题目内容
8.先化简,再求值:(x+2)(x-2)+(2x-1)2-4x(x-1),其中x=2$\sqrt{3}$.分析 先去括号,利用公式法进行计算,并合并同类项,把x的值代入即可.
解答 解:(x+2)(x-2)+(2x-1)2-4x(x-1),
=x2-4+4x2-4x+1-4x2+4x,
=x2-3,
当x=2$\sqrt{3}$时,原式=$(2\sqrt{3})^{2}$-3=12-3=9.
点评 本题考查了整式的混合运算和求值的应用,主要考查学生的化简和计算能力.

练习册系列答案
相关题目
3.对于任意实数m,点P(m-2,9-3m)不可能在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
5.(1)特例导航:请根据所给的运算程序完成填空.
(2)探索与归纳:
如果把你最初任意选择的三个不同的数字分别用a、b、c表示,且a≠b≠c,请再次根据所给运算程序完成填空.
归纳:
从1~9这9个数字中,任意选择3个不同的数字,由这三个数字组成6个不同的三位数(个位数字、十位数字、百位数字互相不重复),把这6个三位数相加,然后用所得的和除以这三个数字的和,结果是222.
(2)探索与归纳:
| 运算程序 | 例如 | 按左侧的形式完成你的举例 |
| ①从1~9这9个数字中,任意选择3个不同的数字 | 3、2、5 | 1、2、3 |
| ②由这三个数字组成6个不同的三位数(个位数字、十位数字、百位数字互相不重复) | 325、352、253、235、523、532 | 123、132、213、231、312、321 |
| ③将②中这6个三位数相加 | 325+352+253+235+523+532=a= 2220 | 1332 |
| ④用③所得的和除以这三个数字的和,得结果 | a÷(3+2+5)= 222 | 222 |
| 运算程序 | 运算过程 |
| ①从1~9这9个数字中,任意选择3个不同的数字 | a、b、c,且a≠b≠c |
| ②由这三个数字组成6个不同的三位数(个位数字、十位数字、百位数字互相不重复) | |
| ③将②中这6个三位数相加 | |
| ④用③所得的和除以这三个数字的和,得结果 |
从1~9这9个数字中,任意选择3个不同的数字,由这三个数字组成6个不同的三位数(个位数字、十位数字、百位数字互相不重复),把这6个三位数相加,然后用所得的和除以这三个数字的和,结果是222.
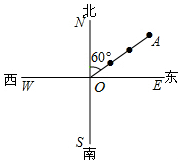 如图,货轮O在航行过程中,在它的北偏东60°方向上,与之相距30海里处发现灯塔A,同时在它的南偏东30°方向上,与之相距20海里处发现货轮B,在它的西南方向上发现客轮C,按下列要求画出.
如图,货轮O在航行过程中,在它的北偏东60°方向上,与之相距30海里处发现灯塔A,同时在它的南偏东30°方向上,与之相距20海里处发现货轮B,在它的西南方向上发现客轮C,按下列要求画出.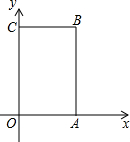 如图,长方形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(2,0)、(0,4).
如图,长方形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(2,0)、(0,4). 如图,在平面直角坐标系xOy中,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象相交于点A(-4,-2),B(m,4),与y轴相交于点C.
如图,在平面直角坐标系xOy中,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象相交于点A(-4,-2),B(m,4),与y轴相交于点C. 如图,图形我们把它称为“8字形”,请说明∠A+∠B=∠C+∠D.
如图,图形我们把它称为“8字形”,请说明∠A+∠B=∠C+∠D.