题目内容
8. 如图,图形我们把它称为“8字形”,请说明∠A+∠B=∠C+∠D.
如图,图形我们把它称为“8字形”,请说明∠A+∠B=∠C+∠D.
分析 先根据三角形内角和等于180°,得出△ABE中,∠A+∠B=180°-∠AEB,△CDE中,∠C+∠D=180°-∠CED,再根据对顶角相等,得出∠AEB=∠DEC,即可得到∠A+∠B=∠C+∠D.
解答 证明:∵三角形内角和等于180°,
∴△ABE中,∠A+∠B=180°-∠AEB,
△CDE中,∠C+∠D=180°-∠CED,
又∵∠AEB=∠DEC,
∴∠A+∠B=∠C+∠D.
点评 本题主要考查了三角形内角和定理的运用,解题时注意:三角形内角和等于180°.

练习册系列答案
相关题目
11.在平面内,下列命题为真命题的是( )
| A. | 四条边相等的四边形是菱形 | B. | 对角线垂直的四边形是菱形 | ||
| C. | 对角线相等的四边形是矩形 | D. | 四个角相等的四边形是正方形 |
13.某男装专营店老板专卖某品牌的夹克,店主统计了一周中不同尺码的夹克销售量如表:
如果店主要购进100件这种夹克,则购进180尺码的夹克数量最合适的是( )
| 尺码 | 170 | 175 | 180 | 185 | 190 |
| 平均每天的销售量/件 | 7 | 9 | 18 | 10 | 6 |
| A. | 20件 | B. | 18件 | C. | 36件 | D. | 50件 |
20.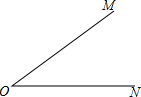 已知∠MON=36°,先以O为圆心,任意长为半径画弧,分别交OM、ON于点A、B,再以A为圆心,AB长为半径画弧,交ON于点C,度量∠ACO的度数为( )
已知∠MON=36°,先以O为圆心,任意长为半径画弧,分别交OM、ON于点A、B,再以A为圆心,AB长为半径画弧,交ON于点C,度量∠ACO的度数为( )
 已知∠MON=36°,先以O为圆心,任意长为半径画弧,分别交OM、ON于点A、B,再以A为圆心,AB长为半径画弧,交ON于点C,度量∠ACO的度数为( )
已知∠MON=36°,先以O为圆心,任意长为半径画弧,分别交OM、ON于点A、B,再以A为圆心,AB长为半径画弧,交ON于点C,度量∠ACO的度数为( )| A. | 36° | B. | 72° | C. | 108° | D. | 180° |
 在四边形ABCD中,对角线AC与BD相交于点O,∠CAB=∠CBD,若BC=3,求AC•CE的值.
在四边形ABCD中,对角线AC与BD相交于点O,∠CAB=∠CBD,若BC=3,求AC•CE的值. 把下面的语句还原成图形:
把下面的语句还原成图形: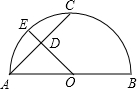 如图,AB为半圆直径,O为圆心,C为半圆上一点,E是弧AC上的一点,且OE⊥AC交弦AC于点D.若AC=8cm,DE=2cm,求OD的长.
如图,AB为半圆直径,O为圆心,C为半圆上一点,E是弧AC上的一点,且OE⊥AC交弦AC于点D.若AC=8cm,DE=2cm,求OD的长.