题目内容
1.设n为自然数,在△ABC内给定n个点.用一些除端点外没有公共点的线段连接这些点及A、B、C,将△ABC分成t个小的三角形.(1)用含n的代数式表示t;
(2)证明t为定值,与线段的连法无关.
分析 (1)先从n=1,2,3开始数出三角形的个数,进而找出规律即可解答;
(2根据三角形的内角和定理和周角的意义即可得出结论.
解答 解:(1)如图1,
当n=1时,t=3=2×1+1,
如图2,
当n=2时,t=3+2=5=2×2+1,
如图3,
当n=3时,t=5+2=2×3+1,
从n=1,2,3发现没多一个点,就多两个三角形
所以,△ABC内给定n个点时,t=2n+1.
(2)由题设得,t个三角形的内角和tπ,△ABC的内角和π,
以给定的n个点的每个点所构成的周角之和n•2π.
由于t个三角形的内角和等于△ABC的内角和与以n个点的每个点所构成的周角之和,
∴tπ=π+n•2π,
∴t=2n+1.
故结论成立.
点评 此题主要考查了三角形的内角和定理,周角的意义,解(1)的关键是从特殊n=1,2,3时小三角形的个数,找出规律,解(2)的关键是用t个小三角形的内角和等于△ABC的内角和与以n个点的每个点所构成的周角之和建立方程.

练习册系列答案
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
1.石墨烯是世界上目前最薄却也最坚硬的纳米材料,还是导电性最好的材料,其理论厚度仅为0.00000000034米,该厚度用科学记数法表示为( )
| A. | 0.34×10-9米 | B. | 34.0×10-11米 | C. | 3.4×10-10米 | D. | 3.4×10-9米 |
13.某男装专营店老板专卖某品牌的夹克,店主统计了一周中不同尺码的夹克销售量如表:
如果店主要购进100件这种夹克,则购进180尺码的夹克数量最合适的是( )
| 尺码 | 170 | 175 | 180 | 185 | 190 |
| 平均每天的销售量/件 | 7 | 9 | 18 | 10 | 6 |
| A. | 20件 | B. | 18件 | C. | 36件 | D. | 50件 |
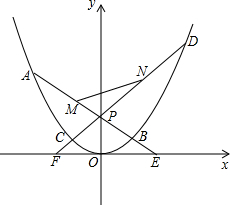 抛物线C0的顶点为原点O,且过点G(2,1).如图,过点P(0,2)分别作两条直线,l1:y=k1x+2和l2:y=k2x+2(其中k1•k2≠0),两直线分别与抛物线、x轴相交于点A、B、E和D、C、F,且M、N分别是AB、CD的中点.
抛物线C0的顶点为原点O,且过点G(2,1).如图,过点P(0,2)分别作两条直线,l1:y=k1x+2和l2:y=k2x+2(其中k1•k2≠0),两直线分别与抛物线、x轴相交于点A、B、E和D、C、F,且M、N分别是AB、CD的中点.