题目内容
11. 如图,已知直线y=-2x+8与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.
如图,已知直线y=-2x+8与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式;
(3)在(2)的条件下,坐标平面内是否存在点P(除点B外),使得△APC与△ABC全等?若存在,直接写出符合条件的点P的坐标;若不存在,请说明理由.
分析 (1)已知直线y=-2x+8与x轴、y轴分别交于点A、C,即可求得A和C的坐标;
(2)根据题意可知△ACD是等腰三角形,算出AD长即可求得D点坐标,最后即可求出CD的解析式;
(3)将点P在不同象限进行分类,根据全等三角形的判定方法找出所有全等三角形,找出符合题意的点P的坐标.
解答 解:(1)令y=0,则-2x+8=0,解得x=4,
∴A(4,0),
令x=0,则y=8,
∴C(0,8);
(2)由折叠可知:CD=AD,
设AD=x,则CD=x,BD=8-x,
由题意得,(8-x)2+42=x2,
解得x=5,
此时AD=5,
∴D(4,5),
设直线CD为y=kx+8,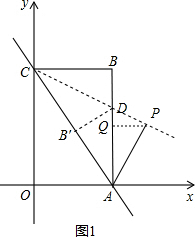
把D(4,5)代入得5=4k+8,解得k=-$\frac{3}{4}$,
∴直线CD的解析式为y=-$\frac{3}{4}$x+8;
(3)①当点P与点O重合时,△APC≌△CBA,此时P(0,0)
②当点P在第一象限时,如图1,
由△APC≌△CBA得∠ACP=∠CAB,
则点P在直线CD上.过P作PQ⊥AD于点Q,
在Rt△ADP中,
AD=5,AP=BC=4,PD=BD=8-5=3,
由AD×PQ=DP×AP得:5PQ=3×4,
∴PQ=$\frac{12}{5}$,
∴xP=4+$\frac{12}{5}$=$\frac{32}{5}$,把x=$\frac{32}{5}$代入y=-$\frac{3}{4}$x+8得y=$\frac{16}{5}$,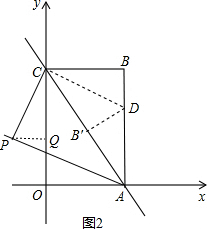
此时P($\frac{32}{5}$,$\frac{16}{5}$)
③当点P在第二象限时,如图2,
同理可求得:PQ=$\frac{12}{5}$,
在RT△PCQ中,CQ=$\sqrt{P{C}^{2}-P{Q}^{2}}$=$\sqrt{{4}^{2}-({\frac{12}{5})}^{2}}$=$\frac{16}{5}$,
∴OQ=8-$\frac{16}{5}$=$\frac{24}{5}$,
此时P(-$\frac{12}{5}$,$\frac{24}{5}$),
综上,满足条件的点P有三个,分别为:(0,0),($\frac{32}{5}$,$\frac{16}{5}$),(-$\frac{12}{5}$,$\frac{24}{5}$).
点评 本题是一次函数的综合题,主要考查了折叠的性质,一次函数图象及其性质,待定系数法求一次函数的解析式,等腰三角形的性质以及全等三角形的判定和性质,分类讨论思想的运用是解题的关键.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案| A. | a2÷a2=a0 | B. | a2+a2=a5 | C. | (a+l)2=a2+l | D. | 3a2-2a2=1 |
 如图,一次函数y=-kx+n(k≠0)与x轴、y轴分别交于A、B两点,与反比例函数y=$\frac{k}{x}$(k≠0)交于C、D两点,且C、D两点分别是线段AB的三等分点,若S△AOB=$\frac{9}{4}$,则n=( )
如图,一次函数y=-kx+n(k≠0)与x轴、y轴分别交于A、B两点,与反比例函数y=$\frac{k}{x}$(k≠0)交于C、D两点,且C、D两点分别是线段AB的三等分点,若S△AOB=$\frac{9}{4}$,则n=( )| A. | -$\sqrt{2}$ | B. | -$\frac{3}{2}\sqrt{2}$ | C. | -2$\sqrt{2}$ | D. | -$\frac{5}{2}\sqrt{2}$ |
 如图,矩形ABCD的对角线AC、BD相交于点0,过点O作OE⊥AC交AB于E.若BC=8,△AOE的面积为20,则sin∠BOE的值为$\frac{3}{5}$.
如图,矩形ABCD的对角线AC、BD相交于点0,过点O作OE⊥AC交AB于E.若BC=8,△AOE的面积为20,则sin∠BOE的值为$\frac{3}{5}$. 如图,a∥b,∠1=∠2,∠3=40°,则∠4等于70度.
如图,a∥b,∠1=∠2,∠3=40°,则∠4等于70度. 如图所示,有以下三个条件:①AC=AB,②AB∥CD,③∠1=∠2,从这三个条件中任选两个作为假设,另一个作为结论,则组成真命题的个数为( )
如图所示,有以下三个条件:①AC=AB,②AB∥CD,③∠1=∠2,从这三个条件中任选两个作为假设,另一个作为结论,则组成真命题的个数为( ) 如图,直线l1、l2、…l6是一组等距离的平行线,过直线l1上的点A作两条射线,分别与直线l3,l6相交于点B、E、C、F.若BC=2,则EF的长是( )
如图,直线l1、l2、…l6是一组等距离的平行线,过直线l1上的点A作两条射线,分别与直线l3,l6相交于点B、E、C、F.若BC=2,则EF的长是( )