题目内容
8.若方程组$\left\{\begin{array}{l}{ax+y=b}\\{2x-by=a}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$,求(a+b)2-(a-b)(a+b).分析 将方程组的解代入方程得到关于a、b的二元一次方程组,解得a、b的值,然后将代数式进行化简,最后将a、b的值代入计算即可.
解答 解:将$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$代入$\left\{\begin{array}{l}{ax+y=b}\\{2x-by=a}\end{array}\right.$得$\left\{\begin{array}{l}{a+1=b}\\{2-b=a}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=\frac{3}{2}}\end{array}\right.$.
∵(a+b)2-(a+b)(a-b)=2b(a+b),
∴当a=$\frac{1}{2}$,b=$\frac{3}{2}$时,原式=2b(a+b)=2×$\frac{3}{2}×2$=6.
点评 本题主要考查的是解二元一次方程组和求代数式的值,根据方程组的解的定义得到关于a、b的方程组,从而求得a、b的值是解题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
13. 如图是一个立体图形及其主视图,则它的俯视图是( )
如图是一个立体图形及其主视图,则它的俯视图是( )
 如图是一个立体图形及其主视图,则它的俯视图是( )
如图是一个立体图形及其主视图,则它的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
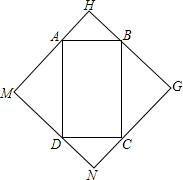 近几年来,石家庄市区的环境越来越美,随处可见的街心花园成为人们休闲的好去处,现二环路办事处又计划将十字路口附近的小块土地进行绿化改造,他们依地势整理出一块矩形区域ABCD,铺成人们可以活动的砖石地面,又分别以AB、BC、CD、DA为斜边向外做等腰直角三角形(如图所示),通过测量,发现四边形MNGH的周长正好是200米,设AB=x米,BC=y米.
近几年来,石家庄市区的环境越来越美,随处可见的街心花园成为人们休闲的好去处,现二环路办事处又计划将十字路口附近的小块土地进行绿化改造,他们依地势整理出一块矩形区域ABCD,铺成人们可以活动的砖石地面,又分别以AB、BC、CD、DA为斜边向外做等腰直角三角形(如图所示),通过测量,发现四边形MNGH的周长正好是200米,设AB=x米,BC=y米. 如图,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(0,1),将线段AB平移,使其一个端点到C(3,2),则平移后另一端点的坐标为(1,3)或(5,1).
如图,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(0,1),将线段AB平移,使其一个端点到C(3,2),则平移后另一端点的坐标为(1,3)或(5,1). 如图,在△ABC中,∠A=50°,E是△ABC内一点,∠BEC=150°,∠ABE的平分线与∠ACE的平分线相交于点D,则∠BDC的度数为多少?
如图,在△ABC中,∠A=50°,E是△ABC内一点,∠BEC=150°,∠ABE的平分线与∠ACE的平分线相交于点D,则∠BDC的度数为多少? 某中学举行中学生“开卷有益”演讲比赛,某同学将选手们的得分情况进行统计,绘成如图所示的得分成绩统计图.
某中学举行中学生“开卷有益”演讲比赛,某同学将选手们的得分情况进行统计,绘成如图所示的得分成绩统计图. 如图,从A地到B地的公路需经过C地,图中AC=50千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A,B两地之间修建一条笔直的公路.
如图,从A地到B地的公路需经过C地,图中AC=50千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A,B两地之间修建一条笔直的公路. x,过点A(0,1)作y轴的垂线交直线
x,过点A(0,1)作y轴的垂线交直线 于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,则点A2015的坐标为( )
于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,则点A2015的坐标为( )