题目内容
20.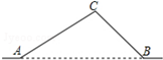 如图,从A地到B地的公路需经过C地,图中AC=50千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A,B两地之间修建一条笔直的公路.
如图,从A地到B地的公路需经过C地,图中AC=50千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A,B两地之间修建一条笔直的公路.(1)求改直的公路AB的长;
(2)问公路改直后比原来缩短了多少千米?(保留到小数点后1位)
(sin25°≈0.42,cos25°≈0.91,tan25°≈0.47,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
分析 (1)作CH⊥AB于H.在Rt△ACH中根据CH=AC•sin∠CAB求出CH的长,由AH=AC•cos∠CAB求出AH的长,同理可得出BH的长,根据AB=AH+BH可得出结论;
(2)根据在Rt△BCH中,BC=CH÷sin∠CBA可得出BC的长,由AC+BC-AB即可得出结论.
解答 解:(1)作CH⊥AB于H.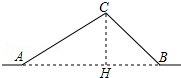
在Rt△ACH中,CH=AC•sin∠CAB=AC•sin25°≈50×0.42=21千米,
AH=AC•cos∠CAB=AC•cos25°≈50×0.91=45.5千米,
在Rt△BCH中,BH=CH÷tan∠CBA=21÷tan37°≈21÷0.75=28千米,
∴AB=AH+BH=45.5+28=73.5千米.
故改直的公路AB的长73.5千米;
(2)在Rt△BCH中,BC=CH÷sin∠CBA=21÷sin37°≈21÷0.6=35千米,
则AC+BC-AB=50+35-73.5=11.5千米.
答:公路改直后比原来缩短了11.5千米.
点评 本题考查的是解直角三角形的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
11.下列四个图形中,是轴对称图形又是中心对称图形的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15. 如图,在边长为1的正方形构成的网络中,半径为1的⊙O的圆心在格点上,则图中阴影部分两个小扇形的面积之和为( )
如图,在边长为1的正方形构成的网络中,半径为1的⊙O的圆心在格点上,则图中阴影部分两个小扇形的面积之和为( )
 如图,在边长为1的正方形构成的网络中,半径为1的⊙O的圆心在格点上,则图中阴影部分两个小扇形的面积之和为( )
如图,在边长为1的正方形构成的网络中,半径为1的⊙O的圆心在格点上,则图中阴影部分两个小扇形的面积之和为( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{8}$ | D. | $\frac{π}{6}$ |
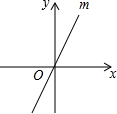 如图,在平面直角坐标系中,直线m经过原点,且与x轴正半轴成60度的角.若点N到x轴、直线m的距离分别为2和1,则点N的坐标为(0,2)或(0,-2)或($\frac{4\sqrt{3}}{3}$,2)或(-$\frac{4\sqrt{3}}{3}$,-2).
如图,在平面直角坐标系中,直线m经过原点,且与x轴正半轴成60度的角.若点N到x轴、直线m的距离分别为2和1,则点N的坐标为(0,2)或(0,-2)或($\frac{4\sqrt{3}}{3}$,2)或(-$\frac{4\sqrt{3}}{3}$,-2).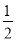 BC的长为半径作弧,两弧交于M,N两点;②作直线MN交AB于点D,连接CD.如果已知CD=AC,∠B=25°,则∠ACB的度数为__________.
BC的长为半径作弧,两弧交于M,N两点;②作直线MN交AB于点D,连接CD.如果已知CD=AC,∠B=25°,则∠ACB的度数为__________.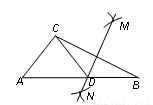
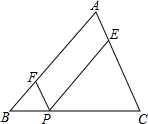 如图,在△ABC中,点P是BC边上任意一点(点P与点B,C不重合),平行四边形AFPE的顶点F,E分别在AB,AC上.已知BC=2,S△ABC=1.设BP=x,平行四边形AFPE的面积为y.
如图,在△ABC中,点P是BC边上任意一点(点P与点B,C不重合),平行四边形AFPE的顶点F,E分别在AB,AC上.已知BC=2,S△ABC=1.设BP=x,平行四边形AFPE的面积为y.