题目内容
14. 如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,此时点C恰好在线段DE上,若∠B=40°,∠CAE=60°,则∠DAC的度数为20°.
如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,此时点C恰好在线段DE上,若∠B=40°,∠CAE=60°,则∠DAC的度数为20°.
分析 由旋转的性质得出得出∠D=∠B=40°,AE=AC,再根据∠CAE=60°,得出△ACE是等边三角形,得出∠ACE=∠E=60°,在△ACD中由三角形外角性质即可求出∠DAC的度数.
解答  解:由旋转的性质得∠D=∠B=40°,AE=AC,
解:由旋转的性质得∠D=∠B=40°,AE=AC,
∵∠CAE=60°,
∴△ACE是等边三角形,
∴∠ACE=∠E=60°,
∵∠ACE是△ACD的外角,
∴∠DAC=∠ACE-∠D=60°-40°=20°.
故答案为:20°
点评 本题以旋转为背景,主要考查了等边三角形的判定与性质以及三角形外角的性质.解题时注意,旋转前、后的图形全等,对应边相等,对应角相等,这是解决问题的关键.

练习册系列答案
相关题目
17.下列图形中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
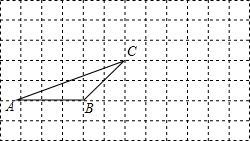 如图:在正方形网格中有一个格点三角形ABC,(即△ABC的各顶点都在格点上),按要求进行下列作图:
如图:在正方形网格中有一个格点三角形ABC,(即△ABC的各顶点都在格点上),按要求进行下列作图: 如图,Rt△ABC中,∠C=90°,∠CAB=37°,AB=5,AC=4,BC=3,直线MN经过点C,交边AB于点D,分别过点A,B作AF⊥MN,BE⊥MN,垂足分别为点E,F,设线段BE,AF的长度分别为d1,d2.
如图,Rt△ABC中,∠C=90°,∠CAB=37°,AB=5,AC=4,BC=3,直线MN经过点C,交边AB于点D,分别过点A,B作AF⊥MN,BE⊥MN,垂足分别为点E,F,设线段BE,AF的长度分别为d1,d2.

 已知:如图,在8×12的矩形网格中,每个小正方形的边长都为1,四边形ABCD的顶点都在格点上.
已知:如图,在8×12的矩形网格中,每个小正方形的边长都为1,四边形ABCD的顶点都在格点上.