Question

19．如图，在平面直角坐标系第一象限中，当m，n为正整数时：

将反比例函数y_n=$\frac{n}{x}$图象上横坐标为m的点叫做“双曲格点”，记作A_[m，n]，例如，点A_[3，2]表示y₂=$\frac{2}{x}$图象上横坐标为3的点，故点A_[3，2]的坐标为（3，$\frac{2}{3}$）．
把y_n=$\frac{n}{x}$的图象沿着y轴平移或以平行于x轴的直线为对称轴进行翻折，将得到的函数图象叫做它的“派生曲线”，例如，图中的曲线f是y₁=$\frac{1}{x}$图象的一条“派生曲线”．
（1）①“双曲格点”A_[2，1]的坐标为（2，$\frac{1}{2}$）；
②若线段A_[4，3]A_[4，n]的长为1，则n=7．
（2）若“双曲格点”A_[m，2]，A_[m+4，m]的纵坐标之和为1，求线段A_[m，2]，A_[m+4，m]的长；
（3）图中的曲线f是y₁=$\frac{1}{x}$图象的一条“派生曲线”，且经过点A_[2，3]，则f的函数表达式为y=$\frac{1}{x}$+1；
（4）已知y₃=$\frac{3}{x}$图象的“派生曲线”g经过“双曲格点”A_[3，3]，且不与y₃=$\frac{3}{x}$的图象重合，试在图中画出g的位置（先描点，再连线）

Answer 1

分析 （1）①根据A_[2，1]表示y₂=$\frac{1}{x}$图象上横坐标为2的点，即可解决问题．
②根据两点间距离公式即可解决问题．
（2）列出方程即可解决问题．
（3）由题意曲线f是y₁=$\frac{1}{x}$图象的向上平移所得，设向上平移a个单位，曲线f解析式为y=$\frac{1}{x}$+a，把（2，$\frac{3}{2}$）代入即可．
（4）由题意y₃=$\frac{3}{x}$图象的“派生曲线”g是由y=$\frac{3}{x}$沿直线y=1翻折得到，由此不能画出图象．

解答 解：（1）①∵A_[2，1]表示y₂=$\frac{1}{x}$图象上横坐标为2的点，
∴A_[2，1]的坐标为（2，$\frac{1}{2}$）．
②由题意|$\frac{3}{4}$-$\frac{n}{4}$|=1，
∵n是正整数，
∴n=7，
故答案为（2，$\frac{1}{2}$），7．

（2）由题意A_[m，2]的坐标为（m，$\frac{2}{m}$）A_[m+4，m]的坐标为（m+4，$\frac{m}{m+4}$），
∴$\frac{2}{m}$+$\frac{m}{m+4}$=1，
解得m=4，
经检验，m=4是分式方程的解．
∴A_[4，2]的坐标为（4，$\frac{1}{2}$）A_[8，4]的坐标为（8，$\frac{1}{2}$），
∴线段A_[m，2]A_[m+4，m]的长为8-4=4．

（3）∵曲线f是y₁=$\frac{1}{x}$图象的一条“派生曲线”，且经过点A_[2，3]，
∴曲线f是y₁=$\frac{1}{x}$图象的向上平移所得，设向上平移a个单位，
∴曲线f解析式为y=$\frac{1}{x}$+a，把（2，$\frac{3}{2}$）代入得到，a=1，
∴f的函数表达式为y=$\frac{1}{x}$+1．

（4）∵y₃=$\frac{3}{x}$图象的“派生曲线”g经过“双曲格点”A_[3，3]，且不与y₃=$\frac{3}{x}$的图象重合，
∴y₃=$\frac{3}{x}$图象的“派生曲线”g是由y=$\frac{3}{x}$沿直线y=1翻折得到，
∴y₃=$\frac{3}{x}$图象的“派生曲线”g经过A_[2，1]，A_[4，5]，
∴y₃=$\frac{3}{x}$图象的“派生曲线”g的图象如图所示，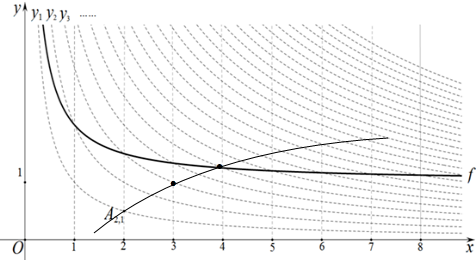

点评 本题考查反比例函数综合题，解题的关键是理解题意，学会用方程的思想思考问题，属于中考创新题目．