题目内容
8.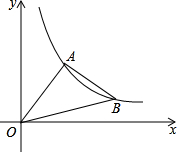 如图,在等腰Rt△ABO中,∠OAB=Rt∠,点A,B都在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,点B在点A的右侧,若点A的横坐标为2,则k的值是2+2$\sqrt{5}$.
如图,在等腰Rt△ABO中,∠OAB=Rt∠,点A,B都在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,点B在点A的右侧,若点A的横坐标为2,则k的值是2+2$\sqrt{5}$.
分析 首先根据已知构造矩形得出△AON≌△BAW,进而得出矩形面积为:S=ON•WN=k+$\frac{{k}^{2}}{4}$,从而得出S△AOB=$\frac{{k}^{2}}{4}$-$\frac{k}{2}$,根据AO=AB,再表示出S△AOB=2+$\frac{{k}^{2}}{8}$,利用两三角形面积相等即可得出k的值.
解答 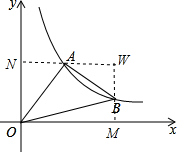 解:过点B作BM⊥x轴于点M,过点A作AN⊥y轴于点N,并延长MB,NA交于一点W,
解:过点B作BM⊥x轴于点M,过点A作AN⊥y轴于点N,并延长MB,NA交于一点W,
∵∠WMO=∠MON=∠WNO=90°,
∴四边形MONW是矩形,
由点A的横坐标为2,则A点坐标为:(2,$\frac{k}{2}$),
∵等腰Rt△OAB中,∠OAB=90°,
∴AB=AO,
∵∠OAB=90°,
∴∠BAW+∠OAN=90°,
∵∠AON+∠OAN=90°,
∴∠BAW=∠AON,
在△AON和△BAW中,
$\left\{\begin{array}{l}{∠W=∠ANO}\\{∠WAB=∠NOA}\\{AB=AO}\end{array}\right.$,
∴△AON≌△BAW(AAS),
∴AW=NO,S△AON=S△BAW,
故WN=AW+AN=2+$\frac{k}{2}$,
∴矩形面积为:S=ON•WN=$\frac{k}{2}$(2+$\frac{k}{2}$)=k+$\frac{{k}^{2}}{4}$,
∵S△MOB=S△AON=S△BAW=$\frac{1}{2}$×2×$\frac{k}{2}$=$\frac{k}{2}$,
∴S△AOB=k+$\frac{{k}^{2}}{4}$-3×$\frac{k}{2}$=$\frac{{k}^{2}}{4}$-$\frac{k}{2}$,
∵AN=2,ON=$\frac{k}{2}$,
∴AB=AO=$\sqrt{4+\frac{{k}^{2}}{4}}$,
∴S△AOB=$\frac{1}{2}$×$\sqrt{4+\frac{{k}^{2}}{4}}$×$\sqrt{4+\frac{{k}^{2}}{4}}$=2+$\frac{{k}^{2}}{8}$,
∴$\frac{{k}^{2}}{4}$-$\frac{k}{2}$=2+$\frac{{k}^{2}}{8}$,
整理得出:
k2-4k-16=0,
解得:k1=2+2$\sqrt{5}$,k2=2-2$\sqrt{5}$(不合题意舍去).
故答案为2+2$\sqrt{5}$.
点评 此题主要考查了反比例函数的综合应用以及全等三角形的判定与性质以及三角形面积求法等知识,根据已知用两种方法得出S△AOB是解题关键.

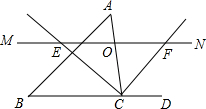 如图,在锐角△ABC中,点O是AC边上的一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,下列结论中正确的是( )
如图,在锐角△ABC中,点O是AC边上的一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,下列结论中正确的是( )①OE=OF;②CE=CF;③若CE=12,CF=5,则OC的长为6;④当AO=CO时,四边形AECF是矩形.
| A. | ①② | B. | ①④ | C. | ①③④ | D. | ②③④ |
| A. | 10 | B. | 5 | C. | 2.5 | D. | 2.4 |
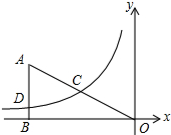 如图,在平面直角坐标系xOy中,过点A(-4,2)向x轴作垂线,垂足为B,联结AO得到△AOB,过边AO中点C的反比例函数$y=\frac{k}{x}$的图象与边AB交于点D.求:
如图,在平面直角坐标系xOy中,过点A(-4,2)向x轴作垂线,垂足为B,联结AO得到△AOB,过边AO中点C的反比例函数$y=\frac{k}{x}$的图象与边AB交于点D.求: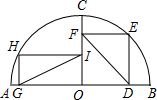 阅读下面材料:
阅读下面材料: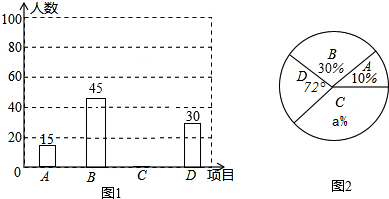
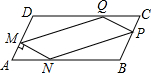 在一块?ABCD的空地上,划一块?MNPQ进行绿化,如图?MNPQ的顶点在?ABCD的边上,已知∠A=60°,∠AMN=90°,且AM=PC=xm,已知?ABCD的边BC=20m,AB=am,a为大于20m的常数,设四边形MNPQ的面积为Sm2.
在一块?ABCD的空地上,划一块?MNPQ进行绿化,如图?MNPQ的顶点在?ABCD的边上,已知∠A=60°,∠AMN=90°,且AM=PC=xm,已知?ABCD的边BC=20m,AB=am,a为大于20m的常数,设四边形MNPQ的面积为Sm2.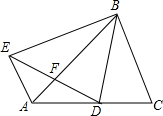 在△ABC中,BD是∠ABC的平分线,在△ABC外取一点E,使得∠EAB=∠ACB,AE=DC,并且线段ED与AB交于点F.求证:EF=DF.
在△ABC中,BD是∠ABC的平分线,在△ABC外取一点E,使得∠EAB=∠ACB,AE=DC,并且线段ED与AB交于点F.求证:EF=DF.