题目内容
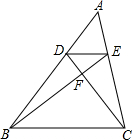如图，D，E分别是△ABC的边AB、AC上的点，且DE∥BC，BE交CD于点F，EF：FB=1：3，且S△DEF=3，则S△ABC的值为（ ）| A、9 | B、27 | C、54 | D、64 |
考点：相似三角形的判定与性质
专题：
分析：作EG⊥BC，FH⊥BC，易证△DEF∽△CBF，可得
=
，再根据
即可求得
的值，即可求得S四边形BCED的面积，根据
即可求得
的值，即可求得
的值，即可解题．
| S△DEF |
| S△BCF |
| 1 |
| 9 |
| BF |
| BE |
| FH |
| EG |
| EF |
| BF |
| DE |
| BC |
| S△ADE |
| S△ABC |
解答：解：作EG⊥BC，FH⊥BC，
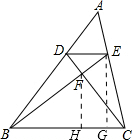
∵DE∥BC，
∴△DEF∽△CBF，
∵
=
，
∴
=
，
∵S△DEF=3，
∴S△BCF=27，
∵
=
=
，
∴S△BCE=
S△BCF，
∴S△CEF=
S△BCF=9，
同理S△BDF=
S△BCF=9，
∴S四边形BCED=48，
∵
=
=
，
∴
=
，
∴S四边形BCED=
S△ABC，
∴S△ABC=54，
故选 C．
∵DE∥BC，
∴△DEF∽△CBF，
∵
| EF |
| BF |
| 1 |
| 3 |
∴
| S△DEF |
| S△BCF |
| 1 |
| 9 |
∵S△DEF=3，
∴S△BCF=27，
∵
| FH |
| EG |
| BF |
| BE |
| 3 |
| 4 |
∴S△BCE=
| 4 |
| 3 |
∴S△CEF=
| 1 |
| 3 |
同理S△BDF=
| 1 |
| 3 |
∴S四边形BCED=48，
∵
| DE |
| BC |
| EF |
| BF |
| 1 |
| 3 |
∴
| S△ADE |
| S△ABC |
| 1 |
| 9 |
∴S四边形BCED=
| 8 |
| 9 |
∴S△ABC=54，
故选 C．
点评：本题考查了相似三角形的判定，考查了相似三角形对应边比例相等的性质，本题中求证△DEF∽△CBF是解题的关键．
练习册系列答案
相关题目
如图，四边形ABCD是矩形，∠EDC=∠CAB，∠DEC=90°，过点B作BF⊥AC于点F，连结EF，求证：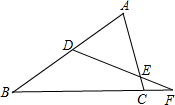
如图，在△ABC中，D是边AB的中点，点E在边AC上，DE、BC的延长线交于点F．求证：
为丰富学生的业余生活，培养学生的兴趣和爱好，某区各个学校开展了学生社团活动，为了解学生参加社团活动情况，对某校七年级学生社团活动进行了抽样调查，制作出如下的统计图，已知该学校七年级学生每人都根据爱好参加一项社团活动．