题目内容
已知一次函数y=(3m-2)x+4-n.
(1)写出m的两个值,使函数y随x的值增大而减小;
(2)m,n为何值时,函数图象经过原点;
(3)你能写出一对使函数图象与y轴的交点在x轴上方的m,n的值吗?试试看.
(1)写出m的两个值,使函数y随x的值增大而减小;
(2)m,n为何值时,函数图象经过原点;
(3)你能写出一对使函数图象与y轴的交点在x轴上方的m,n的值吗?试试看.
考点:一次函数图象与系数的关系
专题:
分析:(1)先根据函数y随x的值增大而减小得出关于m的不等式,求出m的取值范围,再写出符合条件的m的值即可;
(2)根据函数图象经过原点可得出m的取值范围及n的值;
(3)根据函数图象与y轴相交于正半轴的m,n的值值即可.
(2)根据函数图象经过原点可得出m的取值范围及n的值;
(3)根据函数图象与y轴相交于正半轴的m,n的值值即可.
解答:解:(1)∵函数y随x的值增大而减小,
∴3m-2<0,
解得m<
.
∴m的值可以为-1,-2;
(2)∵函数图象经过原点,
∴3m-2≠0,4-n=0,
解得m≠
,n=4;
(3)∵函数图象与y轴的交点在x轴上方,
∴
,
解得m≠
,n<4,
∴m的值可以为1,n的值可以为3.
∴3m-2<0,
解得m<
| 2 |
| 3 |
∴m的值可以为-1,-2;
(2)∵函数图象经过原点,
∴3m-2≠0,4-n=0,
解得m≠
| 2 |
| 3 |
(3)∵函数图象与y轴的交点在x轴上方,
∴
|
解得m≠
| 2 |
| 3 |
∴m的值可以为1,n的值可以为3.
点评:本题考查的是一次函数的图象与系数的关系,熟知一次函数y=kx+b(k≠0)的图象与系数的关系是解答此题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
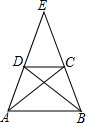 如图,梯形ABCD中,AB∥DC,AC交BD于点F,延长AD、BC交于点E,DE=2,AD=3,求DF:BF的值.
如图,梯形ABCD中,AB∥DC,AC交BD于点F,延长AD、BC交于点E,DE=2,AD=3,求DF:BF的值.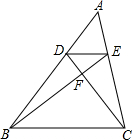 如图,D,E分别是△ABC的边AB、AC上的点,且DE∥BC,BE交CD于点F,EF:FB=1:3,且S△DEF=3,则S△ABC的值为( )
如图,D,E分别是△ABC的边AB、AC上的点,且DE∥BC,BE交CD于点F,EF:FB=1:3,且S△DEF=3,则S△ABC的值为( )