题目内容
6.在研究问题“已知$\left\{\begin{array}{l}{3a+7b+c=4}\\{a-b-3c=8}\end{array}\right.$,求a+b-c的值.”时,三个同学各提出了自己的看法.甲说:“三个未知数,两个方程,条件不够,不能求出abc的值,a+b-c的值很难确定.”;乙说:“是求a+b-c的值,可以把a+b-c看做一个整体,设a+b-c=m,应该可以求解”;丙说:“可以把其中一个未知数c当做已知量,三元一次方程组化为二元一次方程组,从而求出a,b的表达式,再求a+b-c的值”.(1)根据他们的说法,请用合适的方法求a+b-c的值;
(2)若已知b≤c,你能确定c2+a-2b是否有最值?若有,请求出最值和相应的a、b、c的值.
分析 (1)把c当做已知量,三元一次方程组化为二元一次方程组,利用加减消元法求得a=6+2c,b=-2-c,即可求得a+b-c=6+2c-2-c-c=4.
(2)先由b=-2-c,b≤c,求得c的取值,然后把a=6+2c,b=-2-c代入代数式,整理变形为c2+a-2b=(c+2)2+6,根据c的取值即可求得有最小值.
解答 解:(1)原方程组变形为$\left\{\begin{array}{l}{3a+7b=4-c①}\\{a-b=8+3c②}\end{array}\right.$,
①-②×3得,10b=-20-10c,
解得b=-2-c,
把b=-2-c代入②得,a=6+2c,
所以a+b-c=6+2c-2-c-c=4.
(2)∵b=-2-c,b≤c,
∴-2-c≤c,
∴-1≤c,
∵a=6+2c,
∴c2+a-2b
=c2+6+2c-2(-2-c)
=c2+4c+4+6
=(c+2)2+6,
∵c≥-1,
∴当c=-1时,c2+a-2b取取到最小值,
此时a=4,b=-1,c=-1,最小值为7.
点评 本题考查了解三元一次方程组以及二次函数的最值,把c当做已知量,三元一次方程组化为二元一次方程组,利用加减消元法求得a=6+2c,b=-2-c是解题的关键.

练习册系列答案
相关题目
1.如图,从边长为a+2的正方形纸片中剪去一个边长为a-1的正方形(a>1),剩余部分沿虚线剪开,再拼成一个长方形(不重叠无缝隙),则该长方形的面积是( )
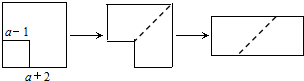

| A. | 4a+1 | B. | 4a+3 | C. | 6a+3 | D. | a2+1 |
11.下列计算正确的是( )
| A. | (-8)-8=0 | B. | (-$\frac{1}{3}$)×(-3)=1 | C. | -(-1)2=1 | D. | |-2|=-2 |
18.某班52名师生准备全部去亮子河旅游,为确定旅游费用,班主任刘老师派班长去了解船只租金情况,班长得到如下表格:
(1)若单租A型船或B型船,至少需多少只?
(2)如果两种船都租,且既不超载也不空载,那么你能设计出几种租船方案?
(3)若你是班长,使总租金最少,应该选择怎样的租船方案?
| A型 | B型 | |
| (人/只) | 5 | 3 |
| (元/只) | 160 | 105 |
(2)如果两种船都租,且既不超载也不空载,那么你能设计出几种租船方案?
(3)若你是班长,使总租金最少,应该选择怎样的租船方案?
9.下列是一元二次方程的是( )
| A. | (x+1)(x-1)=x2-x | B. | ${x^2}-\frac{1}{x}=0$ | C. | ax2+bx+c=0 | D. | x2=0 |
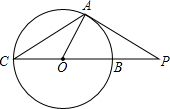 如图,已知CB是⊙O的直径,点A在圆上,且∠AOB=60°,连接OA,过点A作PA⊥OA交CB的延长线于点P,PA=4$\sqrt{3}$.
如图,已知CB是⊙O的直径,点A在圆上,且∠AOB=60°,连接OA,过点A作PA⊥OA交CB的延长线于点P,PA=4$\sqrt{3}$.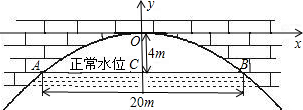 有座抛物线形拱桥(如图),正常水位时桥下河面宽20m,河面距拱顶4m,为了保证过往船只顺利航行,桥下水面的宽度不得小于18m.
有座抛物线形拱桥(如图),正常水位时桥下河面宽20m,河面距拱顶4m,为了保证过往船只顺利航行,桥下水面的宽度不得小于18m.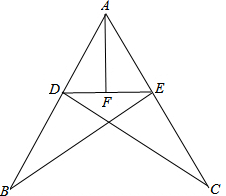 如图,AB=AC,∠B=∠C,点D、E分别在AB、AC上,F是DE的中点.
如图,AB=AC,∠B=∠C,点D、E分别在AB、AC上,F是DE的中点.