题目内容

11．分解因式（2x+3）2-x2的结果是（　　）
A．3（x2+4x+3）B．3（x2+2x+3）C．（3x+3）（x+3）D．3（x+1）（x+3）

分析 直接利用平方差公式分解因式，进而得出答案．

解答 解：（2x+3）2-x2
=（2x+3-x）（2x+3+x）
=（x+3）（3x+3）
=3（x+3）（x+1）．
故选：D．

点评 此题主要考查了公式法分解因式，熟练应用平方差公式是解题关键．

练习册系列答案
相关题目
1．若a2x=25，则a-x等于$±\frac{1}{5}$．
2．下列根式中，是最简根式的是（　　）
A．$\sqrt{\frac{{a}^{3}b}{5}}$B．$\sqrt{{a}^{3}{b}^{2}-a{b}^{2}}$C．$\frac{\sqrt{{a}^{2}+{b}^{2}}}{2}$D．$\sqrt{{a}^{2}-2ab+{b}^{2}}$
19．已知a=16，b=4，则a，b的比例中项为±8．
6．直角三角形的两个锐角平分线与斜边的所夹的锐角之和是（　　）
A．30°B．60°C．45°D．15°和75°
16．计算：$\sqrt{27}+|1-\sqrt{3}|-$（tan30°）-1+（π-2015）0．
3．对下列各整式因式分解正确的是（　　）
A．2x2-x+1=x（2x-1）+1B．x2-2x-1=（x2-1）2
C．2x2-xy-x=2x（x-y-1）D．x2-x-6=（x+2）（x-3）
20．二次函数y=x2+bx+c的图象经过点（4，3），（3，0），求函数y的表达式，并求出当0≤x≤3时，y的最大值．
1．如图，从边长为a+2的正方形纸片中剪去一个边长为a-1的正方形（a＞1），剩余部分沿虚线剪开，再拼成一个长方形（不重叠无缝隙），则该长方形的面积是（　　）
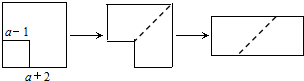
A．4a+1B．4a+3C．6a+3D．a2+1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网