Question

2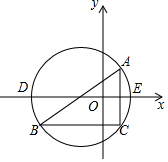．如图，在平面直角坐标系内，已知点A（2，2），B（-6，-4），C（2，-4）．
（1）求△ABC的外接圆的圆心点M的坐标；
（2）求△ABC的外接圆在x轴上所截弦DE的长．

Answer 1

分析 （1）根据三角形的外心是三角形三边垂直平分线的交点解答；
（2）连接OM，作MN⊥DE于N，根据勾股定理求出DN，根据垂径定理求出DE．

解答 解：（1）∵B（-6，-4），C（2，-4），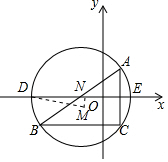
∴线段BC的垂直平分线是x=-2，
∵A（2，2），C（2，-4），
∴线段AC的垂直平分线是y=-1，
∴△ABC的外接圆的圆心M的坐标为：（-2，-1）；
（2）连接OM，作MN⊥DE于N，
由题意得，AC=6，BC=8，
由勾股定理得，AB=10，
则DN=$\sqrt{O{D}^{2}-O{N}^{2}}$=2$\sqrt{6}$，
由垂径定理得，DE=2DN=4$\sqrt{6}$．

点评 本题考查的是三角形的外接圆和外心，掌握三角形的外心的概念、垂径定理的应用是解题的关键．