题目内容
5. 已知Rt△ABC中,∠C=90°,D为AB上的中点.CE⊥AB于E,CD=5,BC=6.求AC,CE的长.
已知Rt△ABC中,∠C=90°,D为AB上的中点.CE⊥AB于E,CD=5,BC=6.求AC,CE的长.
分析 在直角三角形ABC中,由CD为斜边上的中线,得到AB=2CD,求出AB的长,利用勾股定理求出AC的长,直角三角形ABC面积可以由两直角边乘积的一半来求,也可以由斜边乘以斜边上的高来求,根据两直角边与斜边,求出CE的长即可.
解答 解:∵Rt△ABC中,∠C=90°,D为AB上的中点,
∴CD=$\frac{1}{2}$AB,
∵CD=5,
∴AB=10,
由勾股定理得:AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=8,
∵S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CE,即AC•BC=AB•CE,
∴CE=$\frac{AC•BC}{AB}$=$\frac{8×6}{10}$=4.8.
点评 此题考查了勾股定理,直角三角形斜边上的中线,熟练掌握勾股定理是解本题的关键.

练习册系列答案
相关题目
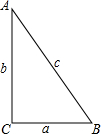 如图,在Rt△ABC中,两直角边长分别为a,b,斜边长为c,若Rt△ABC的面积为3,且a+b=5.则(1)ab=6;(2)c=$\sqrt{13}$.
如图,在Rt△ABC中,两直角边长分别为a,b,斜边长为c,若Rt△ABC的面积为3,且a+b=5.则(1)ab=6;(2)c=$\sqrt{13}$.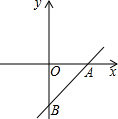 如图所示,已知一次函数y=$\sqrt{3}$x$-\sqrt{3}$分别与x轴、y轴交于A,B两点.求:
如图所示,已知一次函数y=$\sqrt{3}$x$-\sqrt{3}$分别与x轴、y轴交于A,B两点.求: 如图,等腰梯形ABCD中,AB∥DC,AD=BC=8,AB=10,CD=6,则梯形ABCD的面积等于16$\sqrt{15}$.
如图,等腰梯形ABCD中,AB∥DC,AD=BC=8,AB=10,CD=6,则梯形ABCD的面积等于16$\sqrt{15}$.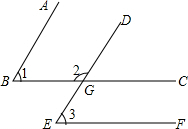 如图,已知∠1=∠3,∠2与∠3互补,AB∥DE吗?BC∥EF吗?为什么?
如图,已知∠1=∠3,∠2与∠3互补,AB∥DE吗?BC∥EF吗?为什么? 如图,已知BE是∠ABC的角平分线,∠1=∠3,你能从图中找到平行的线段吗?请说明理由.
如图,已知BE是∠ABC的角平分线,∠1=∠3,你能从图中找到平行的线段吗?请说明理由.