题目内容
16.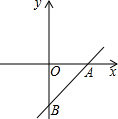 如图所示,已知一次函数y=$\sqrt{3}$x$-\sqrt{3}$分别与x轴、y轴交于A,B两点.求:
如图所示,已知一次函数y=$\sqrt{3}$x$-\sqrt{3}$分别与x轴、y轴交于A,B两点.求:(1)A,B两点的坐标;
(2)∠BAO的度数.
分析 (1)先根据坐标轴上点的坐标特征确定A点坐标为(1,0),B点坐标为(0,-$\sqrt{3}$);
(2)根据正切的定义即可求解.
解答 解:(1)把x=0代入y=$\sqrt{3}$x$-\sqrt{3}$得y=-$\sqrt{3}$;把y=0代入y=$\sqrt{3}$x$-\sqrt{3}$分得$\sqrt{3}$x$-\sqrt{3}$=0,解得x=1,
所以A点坐标为(1,0),B点坐标为(0,-$\sqrt{3}$);
(2)因为A点坐标为(1,0),B点坐标为(0,-$\sqrt{3}$),
所以OA=1,OB=$\sqrt{3}$,
所以tan∠BAO=$\frac{OB}{OA}$=$\frac{\sqrt{3}}{1}$=$\sqrt{3}$,
所以∠BAO=60°.
点评 本题考查了一次函数图象上点的坐标特征:一次函数图象上点的坐标满足其解析式.也考查了锐角三角函数.

练习册系列答案
相关题目
7.用反证法证明命题:在一个三角形中,至少有一个内角不大于60°.证明的第一步是( )
| A. | 假设三个内角都不大于60° | B. | 假设三个内角都大于60° | ||
| C. | 假设三个内角至多有一个大于60° | D. | 假设三个内角至多有两个大于60° |
11.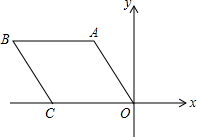 菱形AOCB在平面直角坐标系中的位置如图,若OA=2,∠AOC=45°,则B点的坐标是( )
菱形AOCB在平面直角坐标系中的位置如图,若OA=2,∠AOC=45°,则B点的坐标是( )
 菱形AOCB在平面直角坐标系中的位置如图,若OA=2,∠AOC=45°,则B点的坐标是( )
菱形AOCB在平面直角坐标系中的位置如图,若OA=2,∠AOC=45°,则B点的坐标是( )| A. | (-2-$\sqrt{2}$,$\sqrt{2}$) | B. | (-2+$\sqrt{2}$,$\sqrt{2}$) | C. | (2+$\sqrt{2}$,$\sqrt{2}$) | D. | (2-$\sqrt{2}$,$\sqrt{2}$) |
1. 如图所示,在△ABC中,AB=AC,AB的垂直平分线分别交AC、AB于D、E,若△ABC和△DBC的周长分别为40cm和25cm,则BC等于( )
如图所示,在△ABC中,AB=AC,AB的垂直平分线分别交AC、AB于D、E,若△ABC和△DBC的周长分别为40cm和25cm,则BC等于( )
 如图所示,在△ABC中,AB=AC,AB的垂直平分线分别交AC、AB于D、E,若△ABC和△DBC的周长分别为40cm和25cm,则BC等于( )
如图所示,在△ABC中,AB=AC,AB的垂直平分线分别交AC、AB于D、E,若△ABC和△DBC的周长分别为40cm和25cm,则BC等于( )| A. | 5cm | B. | 10cm | C. | 15cm | D. | 12cm |
8.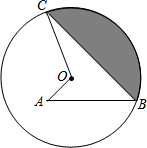 如图,已知点A为⊙O内一点,点B、C均在圆上,∠C=30°,∠A=∠B=45°,线段OA=$\sqrt{3}$-1,则阴影部分的周长为( )
如图,已知点A为⊙O内一点,点B、C均在圆上,∠C=30°,∠A=∠B=45°,线段OA=$\sqrt{3}$-1,则阴影部分的周长为( )
 如图,已知点A为⊙O内一点,点B、C均在圆上,∠C=30°,∠A=∠B=45°,线段OA=$\sqrt{3}$-1,则阴影部分的周长为( )
如图,已知点A为⊙O内一点,点B、C均在圆上,∠C=30°,∠A=∠B=45°,线段OA=$\sqrt{3}$-1,则阴影部分的周长为( )| A. | $\frac{4π}{3}$+2$\sqrt{3}$ | B. | $\frac{2π}{3}$+2$\sqrt{3}$ | C. | $\frac{4π}{3}$+$\sqrt{3}$ | D. | $\frac{2π}{3}$+$\sqrt{3}$ |
 已知Rt△ABC中,∠C=90°,D为AB上的中点.CE⊥AB于E,CD=5,BC=6.求AC,CE的长.
已知Rt△ABC中,∠C=90°,D为AB上的中点.CE⊥AB于E,CD=5,BC=6.求AC,CE的长. “魔术塑料积木”可以开发智力、发挥想像空间.如图是小明用六个棱长为1的立方块组成的一个几何体,其俯视图的面积是5.
“魔术塑料积木”可以开发智力、发挥想像空间.如图是小明用六个棱长为1的立方块组成的一个几何体,其俯视图的面积是5.