题目内容
16．先化简：$\frac{1-a}{a+2}$•$\frac{{a}^{2}-4}{{a}^{2}-2a+1}$÷$\frac{1}{{a}^{2}-1}$，然后选一个你喜欢的a值代入代数式求值．分析 先化简题目中的式子，然后选取一个使得原来的式子有意义的a的值代入即可解答本题，注意a不等于1、-1、-2．
解答 解：$\frac{1-a}{a+2}$•$\frac{{a}^{2}-4}{{a}^{2}-2a+1}$÷$\frac{1}{{a}^{2}-1}$
=$\frac{1-a}{a+2}•\frac{（a+2）（a-2）}{（a-1）^{2}}•（a+1）（a-1）$
=-（a-2）（a+1）
=-a2+a+2，
当a=0时，原式=-02+0+2=2．
点评 本题考查分式的化简求值，解答本题的关键是明确分式化简求值的方法．
练习册系列答案
名校课堂系列答案
相关题目
6．下列各式能用平方差公式计算的（ ）
| A． | （-3a-b） （-3a+b） | B． | （-3a+b） （3a-b） | C． | （3a+b） （-3a-b） | D． | （3a+b） （a-b） |
7．
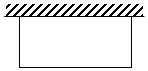用28米长的铁丝围成一个一边靠墙的长方形．
（1）当垂直于墙的一边比另一边少7米时，求长方形的面积．
（2）按表中列出的数据要求，填写表格．
观察表格，你感到长方形的面积会不会有最大的情况？如果会，可能是多少？
用28米长的铁丝围成一个一边靠墙的长方形．（1）当垂直于墙的一边比另一边少7米时，求长方形的面积．
（2）按表中列出的数据要求，填写表格．
观察表格，你感到长方形的面积会不会有最大的情况？如果会，可能是多少？
| 垂直于墙的一边比另一边少（m） | 1 | 4 | 7 | 10 | 13 |
| 长方形的面积 | 90 | 96 | 98 | 96 | 90 |
4．
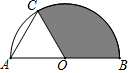如图，AB是半圆O的直径，点C在半圆O上，且△OAC是等边三角形，若AB=12，则图中阴影部分图形的面积为（ ）
如图，AB是半圆O的直径，点C在半圆O上，且△OAC是等边三角形，若AB=12，则图中阴影部分图形的面积为（ ）| A． | 12π | B． | 8π | C． | 24π | D． | 16π |
11．将点A（-1，2）向右平移4个单位长度，再向下平移3个单位长度，则平移后点的坐标是（ ）
| A． | （3，1） | B． | （-3，-1） | C． | （3，-1） | D． | （-3，1） |
1．方程组$\left\{{\begin{array}{l}{{a_1}x+{b_1}y={c_1}}\\{{a_2}x+{b_2}y={c_2}}\end{array}}\right.$的解为$\left\{{\begin{array}{l}{x=4}\\{y=6}\end{array}}\right.$，则方程组$\left\{{\begin{array}{l}{4{a_1}x+3{b_1}y=5{c_1}}\\{4{a_2}x+3{b_2}y=5{c_2}}\end{array}}\right.$的解为（ ）
| A． | $\left\{{\begin{array}{l}{x=4}\\{y=6}\end{array}}\right.$ | B． | $\left\{{\begin{array}{l}{x=5}\\{y=6}\end{array}}\right.$ | C． | $\left\{{\begin{array}{l}{x=5}\\{y=10}\end{array}}\right.$ | D． | $\left\{{\begin{array}{l}{x=10}\\{y=15}\end{array}}\right.$ |
如图所示，在△ABC中，AD为BC边上的中线，且AD平分∠BAC，求证：AB=AC．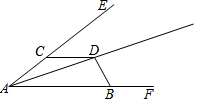
如图，D是∠EAF平分线上一点，点C、B分别在射线AE、AF上且CD=BD（AB＞AC）．
2．
如图，AB∥EF∥CD，EG∥BD，且BD平分∠ABC，则图中与∠1相等的角（∠1除外）共有（ ）
如图，AB∥EF∥CD，EG∥BD，且BD平分∠ABC，则图中与∠1相等的角（∠1除外）共有（ ）| A． | 4个 | B． | 5个 | C． | 6个 | D． | 7个 |