题目内容
7.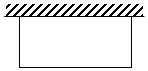 用28米长的铁丝围成一个一边靠墙的长方形.
用28米长的铁丝围成一个一边靠墙的长方形.(1)当垂直于墙的一边比另一边少7米时,求长方形的面积.
(2)按表中列出的数据要求,填写表格.
观察表格,你感到长方形的面积会不会有最大的情况?如果会,可能是多少?
| 垂直于墙的一边比另一边少(m) | 1 | 4 | 7 | 10 | 13 |
| 长方形的面积 | 90 | 96 | 98 | 96 | 90 |
分析 (1)设垂于墙的边长为x,平行于墙边长为y,根据三边长度和为28、垂直于墙的一边比另一边少7米列出关于x、y的方程组,由面积公式可得答案;
(2)与(1)同理可完成表格,设长方形的面积为S,可得S=xy=x(28-2x)=-2x2+28x=-2(x-7)2+98,即可知最值情况.
解答 解:(1)当垂于墙的边长为x,平行于墙边长为y,
∴$\left\{\begin{array}{l}2x+y=28\\ y-x=7\end{array}\right.$,
解得:$\left\{\begin{array}{l}x=7\\ y=14\end{array}\right.$,
∴xy=98,
答:长方形面积为98m2;
(2)完成表格如下:
| 垂直于墙的一边比另一边少(m) | 1 | 4 | 7 | 10 | 13 |
| 长方形的面积 | 90 | 96 | 98 | 96 | 90 |
则S=xy=x(28-2x)=-2x2+28x=-2(x-7)2+98,
∴当x=7时,长方形的面积取得最大值,最大值为98m2.
点评 本题主要考查二次函数的应用和二元一次方程组的应用,根据长宽间的关系列出方程组和函数解析式是解题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
17.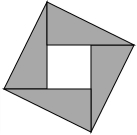 2002年8月在北京召开的国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a,较短直角边为b,则(a+b)2的值为( )
2002年8月在北京召开的国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a,较短直角边为b,则(a+b)2的值为( )
 2002年8月在北京召开的国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a,较短直角边为b,则(a+b)2的值为( )
2002年8月在北京召开的国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a,较短直角边为b,则(a+b)2的值为( )| A. | 25 | B. | 19 | C. | 13 | D. | 169 |
15.如果点P(a-2,3)在y轴上,那么a的值为( )
| A. | 2 | B. | 1 | C. | -2 | D. | 任意数 |
19.一辆汽车在笔直的公路上行驶,两次拐弯后的方向与原来的方向相反,那么两次拐弯的角度可能是( )
| A. | 第一次右拐60°,第二次左拐120° | B. | 第一次左拐60°,第二次右拐60° | ||
| C. | 第一次左拐60°,第二次左拐120° | D. | 第一次右拐60°,第二次右拐60° |
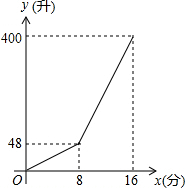 一个容积为400升的水箱,安装A、B两个进水管向水箱注水,注水过程中A水管始终打开,两水管进水的速度保持不变,当水箱注满时,两水管自动停止注水,注水过程中水箱中水量y(升)与A管注水时间x(分)之间的函数图象如图所示.
一个容积为400升的水箱,安装A、B两个进水管向水箱注水,注水过程中A水管始终打开,两水管进水的速度保持不变,当水箱注满时,两水管自动停止注水,注水过程中水箱中水量y(升)与A管注水时间x(分)之间的函数图象如图所示.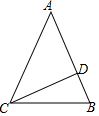 从等腰三角形一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的黄金分割线.
从等腰三角形一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的黄金分割线.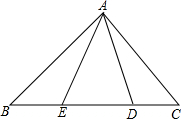 如图,在Rt△ABC中,AB=AC,D、E是斜边BC上的两点,且∠DAE=45°.设BE=a,DC=b,那么AB=$\frac{\sqrt{2}}{2}$(a+b+$\sqrt{{a}^{2}+{b}^{2}}$)(用含a、b的式子表示AB).
如图,在Rt△ABC中,AB=AC,D、E是斜边BC上的两点,且∠DAE=45°.设BE=a,DC=b,那么AB=$\frac{\sqrt{2}}{2}$(a+b+$\sqrt{{a}^{2}+{b}^{2}}$)(用含a、b的式子表示AB).