题目内容
4. 如图所示,在△ABC中,AD为BC边上的中线,且AD平分∠BAC,求证:AB=AC.
如图所示,在△ABC中,AD为BC边上的中线,且AD平分∠BAC,求证:AB=AC.
分析 作DF⊥AB,DE⊥AC,根据三角形的角平分线性质,可得DF=DE,根据“HL”定理,易证Rt△BDE≌Rt△CDF,即可证得.
解答 证明:如图,作DF⊥AB,DE⊥AC,
∵AD平分∠BAC,
∴DE=DF,∠BFD=∠CED=90°,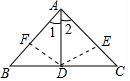
∵D是BC的中点,
∴BD=CD,
在Rt△BDF和Rt△CDE中,
$\left\{\begin{array}{l}{DF=DE}\\{BD=CD}\end{array}\right.$,
∴Rt△BDF≌Rt△CDE(HL),
∴∠B=∠C,
∴AB=AC.
点评 本题主要考查了全等三角形的判定与性质,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具,在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
相关题目
19.一辆汽车在笔直的公路上行驶,两次拐弯后的方向与原来的方向相反,那么两次拐弯的角度可能是( )
| A. | 第一次右拐60°,第二次左拐120° | B. | 第一次左拐60°,第二次右拐60° | ||
| C. | 第一次左拐60°,第二次左拐120° | D. | 第一次右拐60°,第二次右拐60° |
3.在下列图形中,即是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 已知:如图,△ABC中,AD是∠BAC的角平分线,且BD=CD,DE,DF分别垂直于AB,AC,垂足为E,F.求证:AB=AC.
已知:如图,△ABC中,AD是∠BAC的角平分线,且BD=CD,DE,DF分别垂直于AB,AC,垂足为E,F.求证:AB=AC.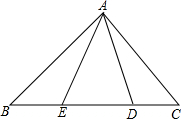 如图,在Rt△ABC中,AB=AC,D、E是斜边BC上的两点,且∠DAE=45°.设BE=a,DC=b,那么AB=$\frac{\sqrt{2}}{2}$(a+b+$\sqrt{{a}^{2}+{b}^{2}}$)(用含a、b的式子表示AB).
如图,在Rt△ABC中,AB=AC,D、E是斜边BC上的两点,且∠DAE=45°.设BE=a,DC=b,那么AB=$\frac{\sqrt{2}}{2}$(a+b+$\sqrt{{a}^{2}+{b}^{2}}$)(用含a、b的式子表示AB). 如图,△ABD是等腰直角三角形,点C是BD延长线上一点,F在AC上,AD=AF,E为△ADC内一点,连接AE,BE,AE平分∠CAD,AE⊥BE.
如图,△ABD是等腰直角三角形,点C是BD延长线上一点,F在AC上,AD=AF,E为△ADC内一点,连接AE,BE,AE平分∠CAD,AE⊥BE.