题目内容
1.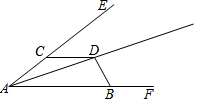 如图,D是∠EAF平分线上一点,点C、B分别在射线AE、AF上且CD=BD(AB>AC).
如图,D是∠EAF平分线上一点,点C、B分别在射线AE、AF上且CD=BD(AB>AC).求证:∠ACD+∠ABD=180°.
分析 本题通过角平分线到角两边距离相等这一性质,再通过三角形的全等证得.
解答 解:过点D分别作AE,AF的垂线,交AE于M,交AF于N
则∠CMD=∠BND=90°,
∵AD是∠EAF的平分线,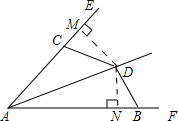
∴DM=DN,
在Rt△CDM和Rt△BDN中,
$\left\{\begin{array}{l}{DM=DN}\\{DC=DB}\end{array}\right.$
∴△CDM≌△BDN,
∴∠CDM=∠BDN,
∴∠MDN=∠CDB,
∵∠ACD+∠MDN=180°,
∴∠ACD+∠ABD=180°.
点评 本题重在考查角平分线上点到角两边距离相等的性质,全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
15.如果点P(a-2,3)在y轴上,那么a的值为( )
| A. | 2 | B. | 1 | C. | -2 | D. | 任意数 |
 已知:如图,△ABC中,AD是∠BAC的角平分线,且BD=CD,DE,DF分别垂直于AB,AC,垂足为E,F.求证:AB=AC.
已知:如图,△ABC中,AD是∠BAC的角平分线,且BD=CD,DE,DF分别垂直于AB,AC,垂足为E,F.求证:AB=AC.
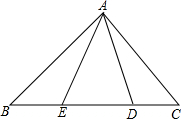 如图,在Rt△ABC中,AB=AC,D、E是斜边BC上的两点,且∠DAE=45°.设BE=a,DC=b,那么AB=$\frac{\sqrt{2}}{2}$(a+b+$\sqrt{{a}^{2}+{b}^{2}}$)(用含a、b的式子表示AB).
如图,在Rt△ABC中,AB=AC,D、E是斜边BC上的两点,且∠DAE=45°.设BE=a,DC=b,那么AB=$\frac{\sqrt{2}}{2}$(a+b+$\sqrt{{a}^{2}+{b}^{2}}$)(用含a、b的式子表示AB).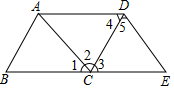 如图,点E在BC的延长线上,下列条件中,
如图,点E在BC的延长线上,下列条件中, 已知Rt△ABC,正方形ABGF,正方形ACDE,BAE共线,FD交AE于I,GE交AF于H,求证:AH=AI.
已知Rt△ABC,正方形ABGF,正方形ACDE,BAE共线,FD交AE于I,GE交AF于H,求证:AH=AI.