题目内容
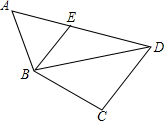 如图,在四边形ABCD中,∠A=58°,∠C=100°,连接BD,E是AD上一点,连接BE,∠EBD=36°.若点A,C分别在线段BE,BD的中垂线上,则∠ADC的度数为( )
如图,在四边形ABCD中,∠A=58°,∠C=100°,连接BD,E是AD上一点,连接BE,∠EBD=36°.若点A,C分别在线段BE,BD的中垂线上,则∠ADC的度数为( )| A、75° | B、65° |
| C、63° | D、61° |
考点:线段垂直平分线的性质
专题:
分析:先根据线段垂直平分线的性质得出AE=AB,BC=DC,再由∠A=58°,∠C=100°得出∠ABE及∠CBD的度数,根据∠EBD=36°得出∠ABC的度数,由四边形内角和定理即可得出结论.
解答:解:∵点A,C分别在线段BE,BD的中垂线上,
∴AE=AB,BC=DC.
∵∠A=58°,∠C=100°,
∴∠ABE=
=61°,∠CBD=
=40°.
∵∠EBD=36°,
∴∠ABC=∠ABE+∠EBD+∠CBD=61°+36°+40°=137°,
∴∠ADC=360°-∠A-∠C-∠ABC=360°-58°-100°-137°=65°.
故答案为:65°.
∴AE=AB,BC=DC.
∵∠A=58°,∠C=100°,
∴∠ABE=
| 180°-58° |
| 2 |
| 180°-100° |
| 2 |
∵∠EBD=36°,
∴∠ABC=∠ABE+∠EBD+∠CBD=61°+36°+40°=137°,
∴∠ADC=360°-∠A-∠C-∠ABC=360°-58°-100°-137°=65°.
故答案为:65°.
点评:本题考查的是线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
已知不等式-x+5>3x-3的解集是2<x,则直线y=-x+5与y=3x-3的交点坐标是( )
| A、(2,3) |
| B、(3,2) |
| C、(3,-2) |
| D、(-3,2) |
 如图所示,已知∠AOC=∠BOC=90°,∠BOE=∠COD,则图中互为余角的角共有( )
如图所示,已知∠AOC=∠BOC=90°,∠BOE=∠COD,则图中互为余角的角共有( )| A、2对 | B、3对 | C、4对 | D、5对 |
给出下列四个函数:y=-3x+1,y=4x-1,y=-
(x>0),y=3x2(x>0),其中y随x的增大而增大的函数有( )
| 3 |
| x |
| A、3个 | B、2个 | C、1个 | D、0个 |
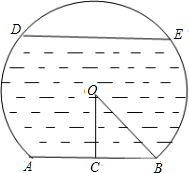 一个弓形桥洞截面示意图如图所示,圆心为O,弦AB是水底线,OC⊥AB,AB=24m,sin∠COB=
一个弓形桥洞截面示意图如图所示,圆心为O,弦AB是水底线,OC⊥AB,AB=24m,sin∠COB=