题目内容
若规定:①{m}表示大于m的最小整数,例如:{3}=4,{-2.4}=-2;②[m]表示不大于m的最大整数,例如:[5]=5,[-3.6]=-4,则使等式{x}-2[x]=4成立的整数x= .
考点:取整计算
专题:
分析:根据题意①{m}表示大于m的最小整数,即2{m}=2(x+1);②[m]表示不大于m的最大整数,即[m]=x.
解答:解:根据题意,得使等式{x}-2[x]=4成立的整数x应满足:
(x+1)-2x=4,
解得:x=-3.
故答案为:-3.
(x+1)-2x=4,
解得:x=-3.
故答案为:-3.
点评:此题主要考查了取整计算,解决此题的关键是理解题意,这里注意x是整数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知样本数据2,4,3,6,5,下列说法不正确的是( )
| A、中位数是3 | B、平均数是4 |
| C、极差是4 | D、方差是2 |
对于二次函数y=2(x-1)2-3,下列说法正确的是( )
| A、图象开口向下 |
| B、图象和y轴交点的纵坐标为-3 |
| C、x<1时,y随x的增大而减小 |
| D、图象的对称轴是直线x=-1 |

 如图,在平面直角坐标系中,抛物线
如图,在平面直角坐标系中,抛物线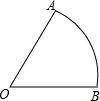 如图,扇形OAB的圆心角为2α,点P为弧AB上一点,将此扇形翻折,当点O和点P重合时折痕恰巧过点B,且
如图,扇形OAB的圆心角为2α,点P为弧AB上一点,将此扇形翻折,当点O和点P重合时折痕恰巧过点B,且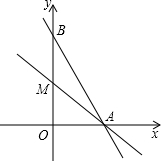 如图,在平面直角坐标系中,函数y=-2x+12的图象分别交x轴、y轴于A、B两点,过点A的直线交y 正半轴于点M,且点M为线段OB的中点.
如图,在平面直角坐标系中,函数y=-2x+12的图象分别交x轴、y轴于A、B两点,过点A的直线交y 正半轴于点M,且点M为线段OB的中点.