题目内容
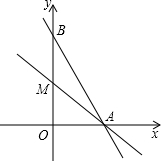 如图,在平面直角坐标系中,函数y=-2x+12的图象分别交x轴、y轴于A、B两点,过点A的直线交y 正半轴于点M,且点M为线段OB的中点.
如图,在平面直角坐标系中,函数y=-2x+12的图象分别交x轴、y轴于A、B两点,过点A的直线交y 正半轴于点M,且点M为线段OB的中点.(1)求直线AM的函数解析式.
(2)试在直线AM上找一点P,使得S△ABP=S△AOM,请直接写出点P的坐标.
(3)点C在直线AM上,在坐标平面内是否存在点D,使以A、O、C、D为顶点的四边形是正方形?若存在,请直接写出点D的坐标;若不存在,请说明理由.
考点:一次函数综合题
专题:
分析:(1)通过函数y=-2x+12求出A、B两点坐标,又由点M为线段OB的中点,即可求得点M的坐标,然后由待定系数法求得直线AM的函数解析式;
(2)设出P点坐标,由两点间的距离公式,可求得AP的长,然后由等腰直角三角形的性质,求得B点到AM的距离,然后由S△ABP=S△AOM,可得方程
×
|x-6|×3
=18,解此方程即可求得答案;
(3)分OA是正方形的一条边和OA是正方形的一条对角线两种情况讨论可得点D的坐标.
(2)设出P点坐标,由两点间的距离公式,可求得AP的长,然后由等腰直角三角形的性质,求得B点到AM的距离,然后由S△ABP=S△AOM,可得方程
| 1 |
| 2 |
| 2 |
| 2 |
(3)分OA是正方形的一条边和OA是正方形的一条对角线两种情况讨论可得点D的坐标.
解答:解:(1)∵直线AB的函数解析式y=-2x+12,
∴A(6,0),B(0,12).
又∵M为线段OB的中点,
∴M(0,6).
设直线AM的解析式为:y=kx+b,则
,
解得:
,
故直线AM的解析式y=-x+6;
 (2)设点P的坐标为:(x,-x+6),
(2)设点P的坐标为:(x,-x+6),
∴AP=
=
|x-6|,
过点B作BH⊥AM于点H,
∵OA=OM,∠AOM=90°,
∴∠AMO=45°,
∴∠BMH=45°,
∴BH=BM•sin45°=6×
=3
,
∵S△ABM=S△AOM,
S△AOM=
OA•OM=
×6×6=18,
S△ABP=
AP•BH=
×
|x-6|×3
,
∴
×
|x-6|×3
=18,
解得:x=0或12,
故点P的坐标为:(0,6)或(12,-6).
(3)当OA是正方形的一条边,以A、O、C、D为顶点的四边形是正方形时,点D的坐标为(6,6);
当OA是正方形的一条对角线,以A、O、C、D为顶点的四边形是正方形时,点D的坐标为(3,-3).
∴A(6,0),B(0,12).
又∵M为线段OB的中点,
∴M(0,6).
设直线AM的解析式为:y=kx+b,则
|
解得:
|
故直线AM的解析式y=-x+6;
 (2)设点P的坐标为:(x,-x+6),
(2)设点P的坐标为:(x,-x+6),∴AP=
| (x-6)2+(-x+6)2 |
| 2 |
过点B作BH⊥AM于点H,
∵OA=OM,∠AOM=90°,
∴∠AMO=45°,
∴∠BMH=45°,
∴BH=BM•sin45°=6×
| ||
| 2 |
| 2 |
∵S△ABM=S△AOM,
S△AOM=
| 1 |
| 2 |
| 1 |
| 2 |
S△ABP=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
∴
| 1 |
| 2 |
| 2 |
| 2 |
解得:x=0或12,
故点P的坐标为:(0,6)或(12,-6).
(3)当OA是正方形的一条边,以A、O、C、D为顶点的四边形是正方形时,点D的坐标为(6,6);
当OA是正方形的一条对角线,以A、O、C、D为顶点的四边形是正方形时,点D的坐标为(3,-3).
点评:此题考查了待定系数法求函数的一次解析式、等腰直角三角形的性质、正方形的性质以及三角形的面积问题.此题难度较大,注意掌握辅助线的作法,注意掌握数形结合思想、分类讨论思想与方程思想的应用.

练习册系列答案
相关题目

 如图,已知AE,DB交于O点,且AB=DE,AE=DB.求证:∠CBO=∠FEO.
如图,已知AE,DB交于O点,且AB=DE,AE=DB.求证:∠CBO=∠FEO.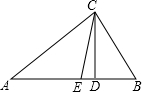 如图,CD、CE分别是△ABC的高和角平分线,∠A=30°,∠B=60°,则∠DCE=
如图,CD、CE分别是△ABC的高和角平分线,∠A=30°,∠B=60°,则∠DCE=