题目内容
如图,在△ABC中,BD平分∠ABC,交AC于点D,BC边上有一点E,连接DE,则AD与DE的关系为( )
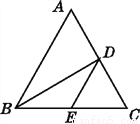
A. AD>DE B. AD=DE
C. AD<DE D. 不确定
D
【解析】根据角平分线上的点到角的两边距离相等可得点D到AB、BC的距离相等，AD、BE都不是点D到AB、BC的距离，大小不确定．
【解析】
∵BD平分∠ABC，
∴点D到AB、BC的距离相等，
∵AD不是点D到AB的距离，点E是BC上一点，
∴AD、DE的大小不确定.
故选D.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，△ABC内有一点D，且DA=DB=DC，若∠DAB=20°，∠DAC=30°，则∠BDC的大小是（ ）
A. 100° B. 80° C. 70° D. 50°
A
【解析】试题分析：如果延长BD交AC于E，由三角形的一个外角等于与它不相邻的两个内角的和，得∠BDC=∠DEC+∠ECD，∠DEC=∠ABE+∠BAE，所以∠BDC=∠ABE+∠BAE+∠ECD，又DA=DB=DC，根据等腰三角形等边对等角的性质得出∠ABE=∠DAB=20°，∠ECD=∠DAC=30°，进而得出结果．
【解析】
延长BD交AC于E．
∵DA=DB=DC，
... 随着锐角α的增大，cosα的值（ ）
A. 增大 B. 减小 C. 不变 D. 增大还是减小不确定
B
【解析】随着锐角α的增大，cosα的值减小．
故选B． 某市出租车收费与行驶路程关系如图所示．如果小明姥姥乘出租车去小明家花去了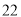
元，那么小明始姥乘车路程为__________千米．
13
【解析】设AB的解析式为y=kx+b，由题意，得，解得： ，
∴直线AB的解析式为y=1.6x+1.2（x≥3），
当y=22时，22=1.6x+1.2，解得：x=13，
故答案为：13． 已知变量y与变量x的关系式为y＝2x－1，则自变量是( )
A. x B. y C. 2 D. －1
A
【解析】∵y＝2x－1，
∴自变量是x.
故选A. 如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,PD=6,则点P到边OB的距离为( )
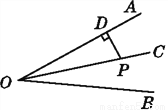
A. 6 B. 5 C. 4 D. 3
A
【解析】试题分析：如图，过点P作PE⊥OB于点E，∵OC是∠AOB的平分线，PD⊥OA于D，∴PE=PD，∵PD=6，∴PE=6，即点P到OB的距离是6．故选A． 如图所示，一测量员站在岸边的A处，刚好正对河岸另一边B处的一棵大树，这位测量员沿河岸向右走了50 m到达C处，在C处测得∠ACB＝38°，求河的宽度．(精确到0.01 m，tan 38°≈0.7813)
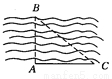
39.07
【解析】试题分析：在直角三角形中，根据已知条件利用所给角的正切值求得AB即可．
试题解析：在Rt△BAC中，∠ACB=38°．
则AB=AC•tan38°≈50×0.7813=39.065≈39.07（米）．
答：河的宽度约为39.07米． 如图，△ABC中，D为AB上一点，E为BC上一点，且AC=CD=BD=BE，∠A=50°，则∠CDE的度数为（ ）
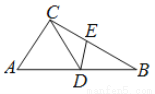
A. 50° B. 51° C. 51.5° D. 52.5°
D
【解析】试题分析：根据等腰三角形的性质推出∠A=∠CDA=50°，∠B=∠DCB，∠BDE=∠BED，根据三角形的外角性质求出∠B=25°，由三角形的内角和定理求出∠BDE=∠BED=（180°﹣25°）=77.5°，，根据平角的定义即可求出∠CDE=180°﹣∠CDA﹣∠EDB=180°﹣50°﹣77.5°=52.5°，故答案选D． 如图，一只蚂蚁在正方形ABCD区域内爬行，点O是对角线的交点，∠MON=90°，OM，ON分别交线段AB，BC于M，N两点，则蚂蚁停留在阴影区域的概率为_____．
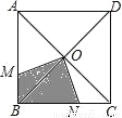
【解析】试题分析：∵四边形ABCD为正方形，点O是对角线的交点，
∴∠MBO=∠NCO=45°，OB=OC，∠BOC=90°，
∵∠MON=90°，
∴∠MOB+∠BON=90°，∠BON+∠NOC=90°，
∴∠MOB=∠NOC．
在△MOB和△NOC中，有，
∴△MOB≌△NOC（ASA）．
同理可得：△AOM≌△BON．
∴S阴影=S△BOC=...