题目内容
如图，每个小正方形的边长为1，A、B、C是小正方形的顶点，求∠ABC的正弦值.
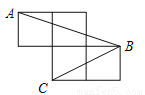
∠ABC的正弦值为
【解析】试题分析：首先利用勾股定理计算出AB2，BC2，AC2，再根据勾股定理逆定理可证明∠BCA=90°，然后得到∠ABC的度数，再利用特殊角的三角函数可得∠ABC的正弦值．
试题解析：连接
AB2=32+12=10，BC2=22+12=5，AC=22+12=5，
∴AC=CB，BC2+AC2=AB2，
∴∠BCA=90°，
∴∠ABC=4...
练习册系列答案
相关题目
如下图，利用关于原点对称的点的坐标的特点，作出与四边形ABCD关于原点对称的图形.
A、B、C、D关于原点对称的点的坐标分别为(2，－3)、(4，－1)、(3，1) (1，0)，图见解析.
【解析】因为关于原点的对称点,横纵坐标都变成相反数,的A,B,C,D关于原点对称的点的坐标分别为:A′（2,－3）,B′（4,－1）,C′（3,1）,D′（1,0）,如图所示:四边形A′B′C′D′即为所求. 一个三角形的三个内角中，锐角的个数最少为 ( )]
A. 0 B. 1 C. 2 D. 3
C
【解析】试题解析：假设在一个三角形中只有1个锐角或一个锐角都没有,则另外的两个角或三个角都大于或等于
于是可得这个三角形的内角和大于
这样违背了三角形的内角和定理，假设不成立，
所以任何一个三角形的三个内角中至少有2个锐角.
故选C. 如图，△ABC内有一点D，且DA=DB=DC，若∠DAB=20°，∠DAC=30°，则∠BDC的大小是（ ）
A. 100° B. 80° C. 70° D. 50°
A
【解析】试题分析：如果延长BD交AC于E，由三角形的一个外角等于与它不相邻的两个内角的和，得∠BDC=∠DEC+∠ECD，∠DEC=∠ABE+∠BAE，所以∠BDC=∠ABE+∠BAE+∠ECD，又DA=DB=DC，根据等腰三角形等边对等角的性质得出∠ABE=∠DAB=20°，∠ECD=∠DAC=30°，进而得出结果．
【解析】
延长BD交AC于E．
∵DA=DB=DC，
... 如图所示，在3×3的正方形网格中已有两个小正方形被涂黑，再将图中其余小正方形任意涂黑一个，使整个图案构成一个轴对称图形的办法有
A．3种 B．4种 C．5种 D．6种
C
【解析】
试题分析：如果一个图形沿一条直线对折，直线两旁的部分能互相重合，那么这个图形叫做轴对称图形．
选择一个正方形涂黑，使得3个涂黑的正方形组成轴对称图形，
选择的位置有以下几种：1处，3处，7处，6处，5处，选择的位置共有5处
故选C. 在Rt△ABC中，∠C＝90°，BC＝3，AC＝4，那么cos A的值等于 ．
．
【解析】
试题分析：∵在Rt△ABC中，∠C=90°，AC=4，BC=3，∴AB==，∴cosA==，故答案为：． 如图，在塔AB前的平地上选择一点C，测出看塔顶的仰角为30°，从C点向塔底走100米到达D点，测出看塔顶的仰角为45°，则塔AB的高为（ ）
A．50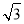
米 B．100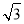米
C．
米 D．
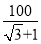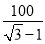米
D.
【解析】
试题解析：在Rt△ABD中，
∵∠ADB=45°，
∴BD=AB．
在Rt△ABC中，
∵∠ACB=30°，
∴=tan30°=，
∴BC=AB．
设AB=x（米），
∵CD=100，
∴BC=x+100．
∴x+100=x
∴x=米．
故选D． 随着锐角α的增大，cosα的值（ ）
A. 增大 B. 减小 C. 不变 D. 增大还是减小不确定
B
【解析】随着锐角α的增大，cosα的值减小．
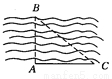
故选B． 如图所示，一测量员站在岸边的A处，刚好正对河岸另一边B处的一棵大树，这位测量员沿河岸向右走了50 m到达C处，在C处测得∠ACB＝38°，求河的宽度．(精确到0.01 m，tan 38°≈0.7813)
39.07
【解析】试题分析：在直角三角形中，根据已知条件利用所给角的正切值求得AB即可．
试题解析：在Rt△BAC中，∠ACB=38°．
则AB=AC•tan38°≈50×0.7813=39.065≈39.07（米）．
答：河的宽度约为39.07米．