Question

3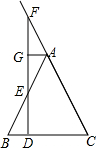．如图，在△ABC中，AB=AC，D是底边BC上的一个动点，过点D作BC的垂线分别交一腰和另一腰的延长线于点E、F，过点A作AG⊥DF于点G．求证：AE=AF．

Answer 1

分析 根据垂直求出∠C+∠F=90°，∠B+∠BEF=90°，再根据等边对等角求出∠B=∠C，从而得到∠F=∠BEF，再根据对顶角相等求出∠BEF=∠AEF，然后求出∠F=∠AEF，根据等角对等边可得AE=AF．

解答 证明：∵FD⊥BC，
∴∠C+∠F=90°，∠B+∠BED=90°，
∵AB=AC，
∴∠B=∠C，
∴∠F=∠BED，
∵∠BED=∠AEF
∴∠F=∠AEF
∴AE=AF．

点评 本题考查了等腰三角形的判定与性质，垂直的定义，三角形中位线定理，平行四边形的判定和性质，熟记等边对等角和等角对等边是解题的关键．