题目内容
13.下列二次根式,不能与$\sqrt{12}$合并的是②⑤(填写序号即可).①$\sqrt{48}$; ②$-\sqrt{125}$; ③$\sqrt{1\frac{1}{3}}$; ④$\frac{\sqrt{3}}{2}$; ⑤$\sqrt{18}$.
分析 先将个二次化简为最简二次根式,然后找出与$\sqrt{12}$被开方数不同的二次根式即可.
解答 解:$\sqrt{12}$=2$\sqrt{3}$,①$\sqrt{48}$=4$\sqrt{3}$,②-$\sqrt{125}$=-5$\sqrt{5}$;③$\sqrt{1\frac{1}{3}}$=$\frac{2\sqrt{3}}{3}$,④$\frac{\sqrt{3}}{2}$,⑤$\sqrt{18}$=3$\sqrt{2}$.
不能与$\sqrt{12}$合并的是-$\sqrt{125}$和$\sqrt{18}$.
故答案为:②⑤.
点评 本题主要考查的是同类二次根式的定义,将各二根式化简为最简二次是解题的关键.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
4.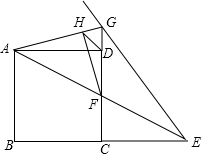 如图,点E是正方形ABCD的边BC延长线一点,连接AE交CD于F,作∠AEG=∠AEB,EG交CD的延长线于G,连接AG,当CE=BC=2时,作FH⊥AG于H,连接DH,则DH的长为( )
如图,点E是正方形ABCD的边BC延长线一点,连接AE交CD于F,作∠AEG=∠AEB,EG交CD的延长线于G,连接AG,当CE=BC=2时,作FH⊥AG于H,连接DH,则DH的长为( )
 如图,点E是正方形ABCD的边BC延长线一点,连接AE交CD于F,作∠AEG=∠AEB,EG交CD的延长线于G,连接AG,当CE=BC=2时,作FH⊥AG于H,连接DH,则DH的长为( )
如图,点E是正方形ABCD的边BC延长线一点,连接AE交CD于F,作∠AEG=∠AEB,EG交CD的延长线于G,连接AG,当CE=BC=2时,作FH⊥AG于H,连接DH,则DH的长为( )| A. | 2-$\sqrt{2}$ | B. | $\sqrt{2}-1$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{2}{3}$ |
5.下列式子正确的是( )
| A. | -52=(-5)×(-5) | B. | 32=3×2 | C. | 32=3+3 | D. | -(-$\frac{1}{2}$)2=-$\frac{1}{2}$×$\frac{1}{2}$ |
 如图,△ABC,按要求完成下列各题:
如图,△ABC,按要求完成下列各题: 如图,边长为8cm的正方形ABCD先向上平移4cm,再向右平移2cm,得到正方形A′B′C′D′,此时阴影部分的面积为24cm2.
如图,边长为8cm的正方形ABCD先向上平移4cm,再向右平移2cm,得到正方形A′B′C′D′,此时阴影部分的面积为24cm2.