题目内容
5．将抛物线y=x2-4x+4沿y轴向下平移9个单位，所得新抛物线与x轴正半轴交于点B，与y轴交于点C，顶点为D．求：（1）点B、C、D坐标；（2）△BCD的面积．分析 （1）首先求得抛物线y=x2-4x+4沿y轴向下平移9个单位后解析式，利用配方法求得D的坐标，令y=0求得C的横坐标，令y=0，解方程求得B的横坐标；
（2）过D作DA⊥y轴于点A，然后根据S△BCD=S梯形AOBD-S△BOC-S△ADC求解．
解答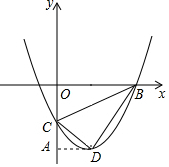 
解：（1）抛物线y=x2-4x+4沿y轴向下平移9个单位后解析式是y=x2-4x+4-9，即y=x2-4x-5．
y=x2-4x-5=（x-2）2-9，
则D的坐标是（2，-9）．
在y=x2-4x-5中令x=0，则y=-5，
则C的坐标是（0，-5），
令y=0，则x2-4x-5=0，
解得x=-1或5，
则B的坐标是（5，0）；
（2）过D作DA⊥y轴于点A．
则S△BCD=S梯形AOBD-S△BOC-S△ADC=$\frac{1}{2}$（2+5）×9-$\frac{1}{2}$×2×4-$\frac{1}{2}$×5×5=15．
点评 本题考查了配方法确定二次函数的顶点坐标，以及函数与x轴、y轴的交点的求法，正确求得抛物线y=x2-4x+4沿y轴向下平移9个单位后解析式是关键．
练习册系列答案
全优点练单元计划系列答案
相关题目
15．
如图，是二次函数y=ax2+bx+c图象的一部分，图象过点A（-3，0），对称轴为直线x=-1，给出四个结论：
①b2＞4ac ②2a+b=0 ③c-a＜0 ④若点B（-4，y1）、C（1，y2）为函数图象上的两点，则y1＜y2，其中正确结论是（ ）
如图，是二次函数y=ax2+bx+c图象的一部分，图象过点A（-3，0），对称轴为直线x=-1，给出四个结论：①b2＞4ac ②2a+b=0 ③c-a＜0 ④若点B（-4，y1）、C（1，y2）为函数图象上的两点，则y1＜y2，其中正确结论是（ ）
| A． | ②④ | B． | ②③ | C． | ①③ | D． | ①④ |
13．在△ABC中，点D、E分别在边AB、AC上，联结DE，那么下列条件中不能判断△ADE和△ABC相似的是（ ）
| A． | DE∥BC | B． | ∠AED=∠B | C． | AE：AD=AB：AC | D． | AE：DE=AC：BC |
10．已知非零向量$\vec a$，$\vec b$，$\vec c$，下列条件中，不能判定$\vec a$∥$\vec b$的是 （ ）
| A． | $\vec a$∥$\vec c$，$\vec b$∥$\vec c$ | B． | $|{\overrightarrow a}|=2|{\overrightarrow b}|$ | C． | $\vec a$=$-2\vec b$ | D． | $\vec a$=$2\vec c$，$\vec b$=$\vec c$ |