题目内容
18. 如图,△ABC中,∠E=18°,BE平分∠ABC,CE平分∠ACD,则∠A等于( )
如图,△ABC中,∠E=18°,BE平分∠ABC,CE平分∠ACD,则∠A等于( )| A. | 36° | B. | 30° | C. | 20° | D. | 18° |
分析 由三角形的一个外角等于与它不相邻的两个内角的和,得∠ACD=∠A+∠ABC,∠ECD=∠E+∠EBC;由角平分线的性质,得∠ECD=$\frac{1}{2}$(∠A+∠ABC),∠EBC=$\frac{1}{2}$∠ABC,利用等量代换,即可求得∠A与∠E的关系,即可得到结论.
解答 证明:∵∠ACD=∠A+∠ABC,
∴∠ECD=$\frac{1}{2}$(∠A+∠ABC).
又∵∠ECD=∠E+∠EBC,
∴∠E+∠EBC=$\frac{1}{2}$(∠A+∠ABC).
∵BE平分∠ABC,
∴∠EBC=$\frac{1}{2}$∠ABC,
∴$\frac{1}{2}$∠ABC+∠E=$\frac{1}{2}$(∠A+∠ABC),
∴∠E=$\frac{1}{2}$∠A=18°,
∴∠A=36°.
故选A.
点评 本题考查了三角形的内角和,三角形外角的性质,三角形的角平分线性质,解答的关键是理清各角之间的关系.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
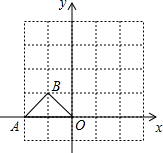 如图,在平面直角坐标系中,△AOB的顶点A(-2,0)、B(-1,1).将△AOB绕点O顺时针旋转90°后,点A、B分别落在A′、B′.
如图,在平面直角坐标系中,△AOB的顶点A(-2,0)、B(-1,1).将△AOB绕点O顺时针旋转90°后,点A、B分别落在A′、B′. 如图,过△ABC的顶点A分别作∠ACB及其外角的平分线的垂线,垂直分布为E、F,连接EF交AB于点M,交AC于点N,求证:
如图,过△ABC的顶点A分别作∠ACB及其外角的平分线的垂线,垂直分布为E、F,连接EF交AB于点M,交AC于点N,求证: 如图,已知平行四边形ABCD中,AB=2$\sqrt{5}$,AD=6,cot∠ABC=$\frac{1}{2}$,将边AB绕点A旋转,使得点B落在平行四边形ABCD的边上,其对应点为B′(点B′不与点B重合),那么sin∠CAB′=$\frac{\sqrt{10}}{10}$或$\frac{\sqrt{2}}{2}$.
如图,已知平行四边形ABCD中,AB=2$\sqrt{5}$,AD=6,cot∠ABC=$\frac{1}{2}$,将边AB绕点A旋转,使得点B落在平行四边形ABCD的边上,其对应点为B′(点B′不与点B重合),那么sin∠CAB′=$\frac{\sqrt{10}}{10}$或$\frac{\sqrt{2}}{2}$.
 如图,已知数轴上有A、B两点(点A在点B的左侧),且两点距离为6个单位长度,动点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.
如图,已知数轴上有A、B两点(点A在点B的左侧),且两点距离为6个单位长度,动点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.