题目内容
6. 如图,已知平行四边形ABCD中,AB=2$\sqrt{5}$,AD=6,cot∠ABC=$\frac{1}{2}$,将边AB绕点A旋转,使得点B落在平行四边形ABCD的边上,其对应点为B′(点B′不与点B重合),那么sin∠CAB′=$\frac{\sqrt{10}}{10}$或$\frac{\sqrt{2}}{2}$.
如图,已知平行四边形ABCD中,AB=2$\sqrt{5}$,AD=6,cot∠ABC=$\frac{1}{2}$,将边AB绕点A旋转,使得点B落在平行四边形ABCD的边上,其对应点为B′(点B′不与点B重合),那么sin∠CAB′=$\frac{\sqrt{10}}{10}$或$\frac{\sqrt{2}}{2}$.
分析 过A作AH⊥BC,连接AC,求得∠ACB的度数,然后分成B′在BC上和在AD上两种情况进行讨论.当点B′落在BC上时,过B′作BM⊥AC,求得B′M的长,利用三角函数定义求得;当B′落在AD上时,∠CAB′=∠ACB,据此即可直接求解.
解答 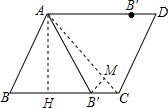 解:过A作AH⊥BC,连接AC.
解:过A作AH⊥BC,连接AC.
cotB=$\frac{BH}{AH}$=$\frac{1}{2}$,则2BH=AH.
∵BH2+AH2=AB2,
∴BH=2,AH=4,
∴HC=BC-BH=6-2=4,
∴AH=HC=4,
∴∠ACB=45°,
①当点B′落在BC上时,
∵直角△ABH和直角△AB′H中,
$\left\{\begin{array}{l}{AB=AB′}\\{AH=AH}\end{array}\right.$,
∴直角△ABH≌直角△AB′H.
∴BH=B′H=2,
∴B′C=2,
∴AC=$\sqrt{A{H}^{2}+H{C}^{2}}$=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$.
过B′作BM⊥AC,
∵∠ACB=45°,
∴△B′MC是等腰直角三角形,
∴B′M=CM=$\sqrt{2}$,
∴sin∠CAB′=$\frac{B′M}{AB′}$=$\frac{\sqrt{2}}{2\sqrt{5}}$=$\frac{\sqrt{10}}{10}$;
②当B′落在AD上时,∠CAB′=∠ACB=45°,
则sin∠CAB′=sin45°=$\frac{\sqrt{2}}{2}$.
总之,sin∠CAB′的值是$\frac{\sqrt{10}}{10}$或$\frac{\sqrt{2}}{2}$.
故答案是:$\frac{\sqrt{10}}{10}$或$\frac{\sqrt{2}}{2}$.
点评 本题考查了旋转的性质以及三角函数的定义,正确分成两种情况进行讨论是解决本题的关键.

 阅读快车系列答案
阅读快车系列答案| 观察时间 | 10:30(t=0) | 10:36(t=6) | 10:48(t=18) |
| 路牌内容 | 上海90Km | 上海80Km | 上海60Km |
 如图,△ABC中,∠E=18°,BE平分∠ABC,CE平分∠ACD,则∠A等于( )
如图,△ABC中,∠E=18°,BE平分∠ABC,CE平分∠ACD,则∠A等于( )| A. | 36° | B. | 30° | C. | 20° | D. | 18° |
 如图,B,E,C,F在同一直线上,且AB=DE,BE=FC,哪一条件可使△ABC≌△DEF( )
如图,B,E,C,F在同一直线上,且AB=DE,BE=FC,哪一条件可使△ABC≌△DEF( )| A. | EF=BC | B. | AC=DF | C. | ∠ACB=∠F | D. | ∠A=∠D |
 某货站用传送带传送货物,为了提高传送过程的安全性,工人师傅将原坡角为45°的传送带AB,调整为坡度i=1:$\sqrt{3}$的新传送带AC(如图所示).已知原传送带AB的长是4$\sqrt{2}$米.那么新传送带AC的长是8米.
某货站用传送带传送货物,为了提高传送过程的安全性,工人师傅将原坡角为45°的传送带AB,调整为坡度i=1:$\sqrt{3}$的新传送带AC(如图所示).已知原传送带AB的长是4$\sqrt{2}$米.那么新传送带AC的长是8米. 在平行四边形ABCD中,点E为AD中点,BE与AC相交于点O,则$\frac{{S}_{△AEO}}{{S}_{四边形DEOC}}$=$\frac{1}{5}$.
在平行四边形ABCD中,点E为AD中点,BE与AC相交于点O,则$\frac{{S}_{△AEO}}{{S}_{四边形DEOC}}$=$\frac{1}{5}$. 如图,在Rt△ABC中,∠B=90°,MN垂直平分AC,与AC、BC分别交于点D、E,连接AE.当AB=3,AC=5时,求△ABE的周长.
如图,在Rt△ABC中,∠B=90°,MN垂直平分AC,与AC、BC分别交于点D、E,连接AE.当AB=3,AC=5时,求△ABE的周长.