题目内容
4. 如图,已知点P是正方形ABCD的对角线BD上的一点.
如图,已知点P是正方形ABCD的对角线BD上的一点.(1)若BP=BC,则∠BPC的度数是67.5°,∠ACP的度数是22.5°.
(2)若CP平分∠ACD,正方形ABCD的边长为1,则DP=$\sqrt{2}$-1.
分析 (1)根据正方形的性质可得到∠DBC=∠BCA=45°,由等腰三角形的性质和三角形内角和定理求出∠BCP=∠BPC=67.5°,从而求得∠ACP的度数;
(2)作PE⊥BD,交CD于E,证明△PDE是等腰直角三角形,得出DP=EP,设DP=PE=x,则DE=$\sqrt{2}$x,再证出EP=EC=x,列出方程,解方程即可.
解答 解:(1)∵四边形ABCD是正方形,
∴∠DBC=∠BCA=∠BDC=∠ACD=45°,
∵BP=BC,
∴∠BCP=∠BPC=(180°-45°)÷2=67.5°,
∴∠ACP=∠BCP-∠BCA=67.5°-45°=22.5°;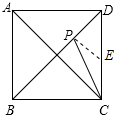 故答案为:67.5°,22.5°.
故答案为:67.5°,22.5°.
(2)作PE⊥BD,交CD于E,如图所示:
则∠DPE=90°,
∵∠BDC=45°,
∴∠PED=45°=∠BDC,
∴DP=EP,
设DP=PE=x,则DE=$\sqrt{2}$x,
∵CP平分∠ACD,∠ACD=45°,
∴∠ECP=22.5°,
∵∠PED=∠ECP+∠EPC,
∴∠EPC=22.5°=∠ECP,
∴EP=EC=x,
∵CD=1,
∴$\sqrt{2}$x+x=1,
解得:x=$\sqrt{2}$-1,
即DP=$\sqrt{2}$-1.
故答案为:$\sqrt{2}$-1.
点评 此题主要考查了正方形的性质、等腰三角形的判定、等腰直角三角形的判定与性质、三角形的外角性质、三角形内角和定理;熟练掌握正方形的性质,通过作辅助线证出DP=EP=EC是解决问题(2)的关键.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
17.估计$\sqrt{11}$的值在( )
| A. | 1和2之间 | B. | 2和3之间 | C. | 3和4之间 | D. | 4和5之间 |
19.下列各数中,绝对值最大的是( )
| A. | 2 | B. | -1 | C. | 0 | D. | -3 |
12.下列运算正确的有( )
| A. | 5ab-ab=4 | B. | 3$\sqrt{2}$-$\sqrt{2}$=3 | C. | $\frac{1}{a}$+$\frac{1}{b}$=$\frac{2}{a+b}$ | D. | a6÷a3=a3 |
 如图,正方形ACEF的边长为2,以AC为一边在同侧做等腰三角形ABC,且∠BAC=150°,BC交AE于点D,下列结论:①EF=ED;②S△DEC=1+$\frac{\sqrt{3}}{3}$;③AD+CD=BD,④S△ABD=$\frac{\sqrt{3}}{3}$,其中正确结论的序号是②③④.
如图,正方形ACEF的边长为2,以AC为一边在同侧做等腰三角形ABC,且∠BAC=150°,BC交AE于点D,下列结论:①EF=ED;②S△DEC=1+$\frac{\sqrt{3}}{3}$;③AD+CD=BD,④S△ABD=$\frac{\sqrt{3}}{3}$,其中正确结论的序号是②③④.