题目内容
11.已知,m,n是一元二次方程x2+4x+3=0的两个实数根,且|m|<|n|,抛物线y=x2+bx+c的图象经过点A(m,0),B(0,n),如图所示.(1)求这个抛物线的解析式;
(2)设(1)中的抛物线与x轴的另一个交点为C,抛物线的顶点为D,试求出点C,D的坐标,并判断△BCD的形状;
(3)点P是直线BC上的一个动点(点P不与点B和点C重合),过点P作x轴的垂线,交抛物线于点M,点Q在直线BC上,距离点P为$\sqrt{2}$个单位长度,设点P的横坐标为t,△PMQ的面积为S,求出S与t之间的函数关系式.

分析 (1)先解一元二次方程,然后用待定系数法求出抛物线解析式;
(2)先解方程求出抛物线与x轴的交点,再判断出△BOC和△BED都是等腰直角三角形,从而得到结论;
(3)先求出QF=1,再分两种情况,当点P在点M上方和下方,分别计算即可.
解答 解(1)∵x2+4x+3=0,
∴x1=-1,x2=-3,
∵m,n是一元二次方程x2+4x+3=0的两个实数根,且|m|<|n|,
∴m=-1,n=-3,
∵抛物线y=x2+bx+c的图象经过点A(m,0),B(0,n),
∴$\left\{\begin{array}{l}{1-b+c=0}\\{c=-3}\end{array}\right.$,
∴$\left\{\begin{array}{l}{b=-2}\\{c=-3}\end{array}\right.$,
∴抛物线解析式为y=x2-2x-3,
(2)令y=0,则x2-2x-3=0,
∴x1=-1,x2=3,
∴C(3,0),
∵y=x2-2x-3=(x-1)2-4,
∴顶点坐标D(1,-4),
过点D作DE⊥y轴,
∵OB=OC=3,
∴BE=DE=1,
∴△BOC和△BED都是等腰直角三角形,
∴∠OBC=∠DBE=45°,
∴∠CBD=90°,
∴△BCD是直角三角形;
(3)如图,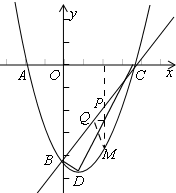
∵B(0,-3),C(3,0),
∴直线BC解析式为y=x-3,
∵点P的横坐标为t,PM⊥x轴,
∴点M的横坐标为t,
∵点P在直线BC上,点M在抛物线上,
∴P(t,t-3),M(t,t2-2t-3),
过点Q作QF⊥PM,
∴△PQF是等腰直角三角形,
∵PQ=$\sqrt{2}$,
∴QF=1,
当点P在点M上方时,即0<t<3时,
PM=t-3-(t2-2t-3)=-t2+3t,
∴S=$\frac{1}{2}$PM×QF=$\frac{1}{2}$(-t2-3t)=-$\frac{1}{2}$t2+$\frac{3}{2}$t,
如图3,当点P在点M下方时,即t<0或t>3时,
PM=t2-2t-3-(t-3),
∴S=$\frac{1}{2}$PM×QF=$\frac{1}{2}$(t2-3t)=$\frac{1}{2}$t2-$\frac{3}{2}$t
点评 此题是二次函数综合题,主要考查了一元二次方程的解法,待定系数法求函数解析式,等腰直角三角形的性质和判定,解本题的关键是判定△BCD是直角三角形.

 如图,矩形ABCD中,AB=3,AD=4,BE⊥AC,则BE长为( )
如图,矩形ABCD中,AB=3,AD=4,BE⊥AC,则BE长为( )| A. | 5 | B. | $\frac{12}{5}$ | C. | $\frac{9}{5}$ | D. | $\frac{5}{2}$ |
| x | … | -3 | -2 | -1 | 0 | 1 | … |
| y | … | -3 | -2 | -3 | -6 | -11 | … |
| A. | 直线x=-3 | B. | 直线x=-2 | C. | 直线x=-1 | D. | 直线x=0 |
| A. | 1次 | B. | 2次 | C. | 3次 | D. | 4次 |
 如图,已知点P是正方形ABCD的对角线BD上的一点.
如图,已知点P是正方形ABCD的对角线BD上的一点. 如图,已知点A、C在反比例函数y=$\frac{a}{x}$的图象上,点B,D在反比例函数y=$\frac{b}{x}$的图象上,a>b>0,AB∥CD∥x轴,AB,CD在x轴的两侧,AB=$\frac{3}{4}$,CD=$\frac{3}{2}$,AB与CD间的距离为6,则a-b的值是3.
如图,已知点A、C在反比例函数y=$\frac{a}{x}$的图象上,点B,D在反比例函数y=$\frac{b}{x}$的图象上,a>b>0,AB∥CD∥x轴,AB,CD在x轴的两侧,AB=$\frac{3}{4}$,CD=$\frac{3}{2}$,AB与CD间的距离为6,则a-b的值是3.