题目内容
16．若关于x的方程x2+（k-2）x-k2=0的两根互为相反数，则k=2．分析 利用x1+x2=-$\frac{b}{a}$可得到-（k-2）=0，然后解一元一次方程即可．
解答 解：根据题意得-（k-2）=0，
解得k=2．
故答案为2．
点评 本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$．
练习册系列答案
浙江名校名师金卷系列答案
全优冲刺100分系列答案
相关题目
8．已知⊙O的半径为r，其内接正六边形，正四边形，正三角形的边长分别为a，b，c，则a：b：c的值为（ ）
| A． | 1：2：3 | B． | 3：2：1 | C． | 1：$\sqrt{2}$：$\sqrt{3}$ | D． | $\sqrt{3}$：$\sqrt{2}$：1 |
如图，已知点P是正方形ABCD的对角线BD上的一点．
1．下列各数中，与3互为相反数的是（ ）
| A． | $\frac{1}{3}$ | B． | -3 | C． | 3-1 | D． | -$\frac{1}{3}$ |
7．
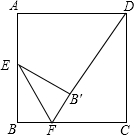如图，正方形ABCD边长为2，E为AB边的中点，点F是BC边上一个动点，把△BEF沿EF向形内部折叠，点B的对应点为B′，当B′D的长最小时，BF长为（ ）
如图，正方形ABCD边长为2，E为AB边的中点，点F是BC边上一个动点，把△BEF沿EF向形内部折叠，点B的对应点为B′，当B′D的长最小时，BF长为（ ）| A． | $\frac{\sqrt{5}}{2}$ | B． | $\sqrt{5}$-1 | C． | $\frac{\sqrt{5}-1}{2}$ | D． | $\frac{\sqrt{5}+1}{2}$ |
3．
如图，矩形ABCD中，AB=3，AD=4，BE⊥AC，则BE长为（ ）
如图，矩形ABCD中，AB=3，AD=4，BE⊥AC，则BE长为（ ）| A． | 5 | B． | $\frac{12}{5}$ | C． | $\frac{9}{5}$ | D． | $\frac{5}{2}$ |