题目内容
11.已知a、b、c满足等式a2-4b=8,b2-6c=-14,c2-8a=-23,则(a-b)c=8.分析 将已知三个等式的左右分别相加,然后根据配方法将a2-4b+b2-6c+c2-8a转化为偶次方的和的形式(a-4)2+(b-2)2+(c-3)2=0;最后根据非负数的性质解答即可.
解答 解:∵a2-4b=8,b2-6c=-14,c2-8a=-23,
∴a2-4b+b2-6c+c2-8a=-29,
∴(a2-8a+16)+(b2-4b+4)+(c2-6c+9)=0,
即(a-4)2+(b-2)2+(c-3)2=0,
∴a-4=0,b-2=0,c-3=0,
∴a=4,b=2,c=3,
∴(a-b)c=8.
故答案为:8.
点评 本题考查了配方法的应用、非负数的性质:偶次方,解题的关键是根据完全平方和公式将代数式转化为偶次方的和的形式,求出a,b,c的值.

练习册系列答案
相关题目
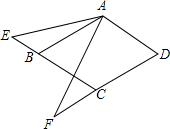 如图,菱形ABCD中,AB=a,∠ABC=60°,点E、F分别在CB、DC的延长线上,∠EAF=60°.
如图,菱形ABCD中,AB=a,∠ABC=60°,点E、F分别在CB、DC的延长线上,∠EAF=60°. 学校的生物老师想利用一边长为15米的墙及可以围成24米长的建筑材料,建造一间“小动物之家”,如图所示,它的平面图是长方形,请你帮老师计算一下,小动物之家的面积能否为32平方米.
学校的生物老师想利用一边长为15米的墙及可以围成24米长的建筑材料,建造一间“小动物之家”,如图所示,它的平面图是长方形,请你帮老师计算一下,小动物之家的面积能否为32平方米. 如图,在等腰△ABC中,AB=CB,M为△ABC内一点,∠MAC+∠MCB=∠MCA=30°,则∠BMC的度数为150°.
如图,在等腰△ABC中,AB=CB,M为△ABC内一点,∠MAC+∠MCB=∠MCA=30°,则∠BMC的度数为150°.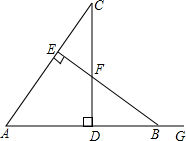 如图,CD⊥AB于点D,BE⊥AC于点E,△ABE≌△ACD,∠C=20°,AB=10,AD=6,G为AB延长线上一点,求∠EBG的度数和CE的长.
如图,CD⊥AB于点D,BE⊥AC于点E,△ABE≌△ACD,∠C=20°,AB=10,AD=6,G为AB延长线上一点,求∠EBG的度数和CE的长. 如图,在△ABC中,点E、F分别在BC,AB上,且DE∥AB,EF∥AC.
如图,在△ABC中,点E、F分别在BC,AB上,且DE∥AB,EF∥AC. 如图,AE平分∠BAD,DE平分∠ADC,AB⊥BC于B,且DE⊥EA于E,试说明DC⊥BC.
如图,AE平分∠BAD,DE平分∠ADC,AB⊥BC于B,且DE⊥EA于E,试说明DC⊥BC.