题目内容
6.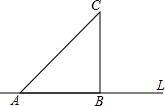 如图,等腰直角三角形ABC的一直角边AB在直线L上,将该三角形绕着顶点B顺时针方向旋转,至边BC落在直线L上,再绕顶点C顺时针旋转至边CA落在直线L上,若AB=1,则顶点A的运动轨迹与直线L围成的图形的面积是π+$\frac{1}{2}$.
如图,等腰直角三角形ABC的一直角边AB在直线L上,将该三角形绕着顶点B顺时针方向旋转,至边BC落在直线L上,再绕顶点C顺时针旋转至边CA落在直线L上,若AB=1,则顶点A的运动轨迹与直线L围成的图形的面积是π+$\frac{1}{2}$.
分析 在等腰直角三角形ABC中,AB=1,根据勾股定理得到AC的长为$\sqrt{2}$,求出∠BC1C=∠BCA、∠A1C1C,顶点A运动到点A1的位置时,点A经过的路线与直线l所围成的面积是两个扇形的面积+△BCC1的面积.根据扇形的面积公式可以进行计算.
解答 解:如图,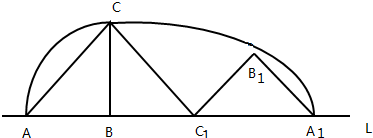
在等腰直角三角形ABC中,∵AB=1,
∴AC=$\sqrt{2}$,∠BCA=45°,
由旋转性质可知,CC1=AC=$\sqrt{2}$,∠BC1C=∠BCA=45°
∴∠A1C1C=135°,
则S=$\frac{90π•{1}^{2}}{360}$+$\frac{1}{2}$×1×1+$\frac{135π•(\sqrt{2})^{2}}{360}$
=π+$\frac{1}{2}$,
故答案为:π+$\frac{1}{2}$.
点评 本题考查了扇形的面积计算、勾股定理、旋转的性质的应用,本题的关键是弄清顶点A运动到点A1的位置时,点A经过的路线与直线l所围成的图形的形状.

练习册系列答案
相关题目
8.下列运算正确的是( )
| A. | x4+x2=x6 | B. | x2•x3=x6 | C. | (x2)3=x6 | D. | x2-y2=(x-y)2 |
5.某个密码锁的密码由三个数字组成,每个数字都是0-9这十个数字中的一个,只有当三个数字与所设定的密码及顺序完全相同时,才能将锁打开.如果仅忘记了锁设密码的最后那个数字,那么一次就能打开该密码的概率是( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
11. 如图,点C在以AB为直径的⊙O上(点C不与A、B重合),点E在弦AC上,EF⊥AB于点F,若∠B=66°,则∠AEF的大小为( )
如图,点C在以AB为直径的⊙O上(点C不与A、B重合),点E在弦AC上,EF⊥AB于点F,若∠B=66°,则∠AEF的大小为( )
 如图,点C在以AB为直径的⊙O上(点C不与A、B重合),点E在弦AC上,EF⊥AB于点F,若∠B=66°,则∠AEF的大小为( )
如图,点C在以AB为直径的⊙O上(点C不与A、B重合),点E在弦AC上,EF⊥AB于点F,若∠B=66°,则∠AEF的大小为( )| A. | 24° | B. | 33° | C. | 66° | D. | 76° |
15.已知等腰三角形的一边长为3cm,且它的周长为12cm,则它的底边长为( )
| A. | 3cm | B. | 6cm | C. | 9cm | D. | 3cm或6cm |
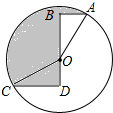 如图,⊙O的半径为2,点A、C在⊙O上,线段BD经过圆心O,∠ABD=∠CDB=90°,AB=1,CD=$\sqrt{3}$,则图中阴影部分的面积为$\frac{5}{3}$π.
如图,⊙O的半径为2,点A、C在⊙O上,线段BD经过圆心O,∠ABD=∠CDB=90°,AB=1,CD=$\sqrt{3}$,则图中阴影部分的面积为$\frac{5}{3}$π.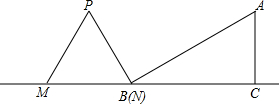
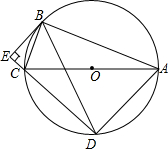 如图,⊙O是△ABC的外接圆,AC是⊙O的直径,弦BD=BA,AB=12,BC=5,BE⊥DC,交DC的延长线于点E.
如图,⊙O是△ABC的外接圆,AC是⊙O的直径,弦BD=BA,AB=12,BC=5,BE⊥DC,交DC的延长线于点E.