题目内容
15.已知$\left\{\begin{array}{l}{{y}^{2}=8x}\\{{x}^{2}=8y}\end{array}\right.$,求这两个抛物线的交点坐标.分析 把②代入①得:$\frac{{x}^{4}}{64}$=8x,分别讨论x=0和x≠0两种情况,求出x和y的值即可.
解答 解:$\left\{\begin{array}{l}{{y}^{2}=8x①}\\{{x}^{2}=8y②}\end{array}\right.$,
把②代入①得:$\frac{{x}^{4}}{64}$=8x,
当x=0时,y=0,
当x≠0时,
即x3=64×8,
解得x=8,
把x=8代入②得到y=8,
即这两个抛物线的交点坐标为(0,0)和(8,8).
点评 本题主要考查了二次函数的性质,解答本题的关键是会消元法解方程组,此题难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.9的平方根是( )
| A. | ±3 | B. | 3 | C. | -33 | D. | $\sqrt{3}$ |
3.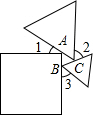 一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=( )
一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=( )
 一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=( )
一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=( )| A. | 100° | B. | 120° | C. | 130° | D. | 180° |
20.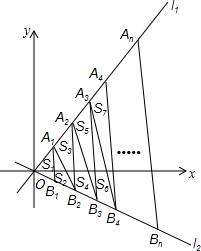 如图,直线l1的解析式为y1=$\sqrt{3}$x,直线l2的解析式为y2=-$\frac{\sqrt{3}}{3}$x,过点(1,0)、(2,0)、(3,0)、(4,0)…(n,0)作y轴的平行线,与直线l1分别交于点A1、A2、A3、A4、…An,与直线l2分别交于点B1、B2、B3、…Bn,连接A1B2、A2B3、A3B4、…、AnBn+1,设△OA1B1的面积为S1,△A1B1B2的面积为S2,△A1B2A2的面积为S3…,则S2015=( )
如图,直线l1的解析式为y1=$\sqrt{3}$x,直线l2的解析式为y2=-$\frac{\sqrt{3}}{3}$x,过点(1,0)、(2,0)、(3,0)、(4,0)…(n,0)作y轴的平行线,与直线l1分别交于点A1、A2、A3、A4、…An,与直线l2分别交于点B1、B2、B3、…Bn,连接A1B2、A2B3、A3B4、…、AnBn+1,设△OA1B1的面积为S1,△A1B1B2的面积为S2,△A1B2A2的面积为S3…,则S2015=( )
 如图,直线l1的解析式为y1=$\sqrt{3}$x,直线l2的解析式为y2=-$\frac{\sqrt{3}}{3}$x,过点(1,0)、(2,0)、(3,0)、(4,0)…(n,0)作y轴的平行线,与直线l1分别交于点A1、A2、A3、A4、…An,与直线l2分别交于点B1、B2、B3、…Bn,连接A1B2、A2B3、A3B4、…、AnBn+1,设△OA1B1的面积为S1,△A1B1B2的面积为S2,△A1B2A2的面积为S3…,则S2015=( )
如图,直线l1的解析式为y1=$\sqrt{3}$x,直线l2的解析式为y2=-$\frac{\sqrt{3}}{3}$x,过点(1,0)、(2,0)、(3,0)、(4,0)…(n,0)作y轴的平行线,与直线l1分别交于点A1、A2、A3、A4、…An,与直线l2分别交于点B1、B2、B3、…Bn,连接A1B2、A2B3、A3B4、…、AnBn+1,设△OA1B1的面积为S1,△A1B1B2的面积为S2,△A1B2A2的面积为S3…,则S2015=( )| A. | $\frac{2016\sqrt{3}}{3}$ | B. | 1008$\sqrt{3}$ | C. | $\frac{2015\sqrt{3}}{2}$ | D. | $\frac{2015\sqrt{3}}{3}$ |
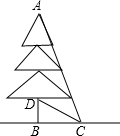 某小区在绿化改造项目中,要将一棵已经枯萎的树砍伐掉.在操作过程中,李师傅想直接从根部把树放倒,张师傅不同意,他担心这样会损坏这棵树周围10米处的花园和雕塑.通过测量知道图中∠BCD=30°,∠DCA=35°,BD=3米,根据计算说明张师傅的担心是否有必要?(结果精确到0.1位,tan65°≈2.1)
某小区在绿化改造项目中,要将一棵已经枯萎的树砍伐掉.在操作过程中,李师傅想直接从根部把树放倒,张师傅不同意,他担心这样会损坏这棵树周围10米处的花园和雕塑.通过测量知道图中∠BCD=30°,∠DCA=35°,BD=3米,根据计算说明张师傅的担心是否有必要?(结果精确到0.1位,tan65°≈2.1) 如图,△ABC是边长为$\sqrt{3}$的等边三角形,点P.Q分别是射线AB、BC上两个动点,且AP=CQ,PQ交AC与D,作PE丄AC于E,那么DE的长度为$\frac{1}{2}$$\sqrt{3}$.
如图,△ABC是边长为$\sqrt{3}$的等边三角形,点P.Q分别是射线AB、BC上两个动点,且AP=CQ,PQ交AC与D,作PE丄AC于E,那么DE的长度为$\frac{1}{2}$$\sqrt{3}$.