题目内容
5.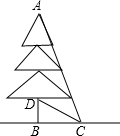 某小区在绿化改造项目中,要将一棵已经枯萎的树砍伐掉.在操作过程中,李师傅想直接从根部把树放倒,张师傅不同意,他担心这样会损坏这棵树周围10米处的花园和雕塑.通过测量知道图中∠BCD=30°,∠DCA=35°,BD=3米,根据计算说明张师傅的担心是否有必要?(结果精确到0.1位,tan65°≈2.1)
某小区在绿化改造项目中,要将一棵已经枯萎的树砍伐掉.在操作过程中,李师傅想直接从根部把树放倒,张师傅不同意,他担心这样会损坏这棵树周围10米处的花园和雕塑.通过测量知道图中∠BCD=30°,∠DCA=35°,BD=3米,根据计算说明张师傅的担心是否有必要?(结果精确到0.1位,tan65°≈2.1)
分析 根据特殊角的三角函数值求出BC长,再利用65°的正切值可得树高AB,与10进行比较,即可得出答案.
解答 解:∵BD=3米,∠BCD=30°,∠ABC=90°,
∴BC=BD÷tan30°=3$\sqrt{3}$(米);
∵∠DCA=35°,
∴∠ACB=65°,
∴AB=BC×tan65°=3$\sqrt{3}$×2.1≈11.1米,
∵11.1>10,
∴张师傅的担心有必要的.
点评 本题考查解直角三角形在实际生活中的应用,题目新颖,得到两个直角三角形的公共边的长度是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13. 如图,△ABC中,E为边BC延长线上一点,∠ABC的平分线与∠ACE的平分线交于点D,若∠A=46°,则∠D的度数为( )
如图,△ABC中,E为边BC延长线上一点,∠ABC的平分线与∠ACE的平分线交于点D,若∠A=46°,则∠D的度数为( )
 如图,△ABC中,E为边BC延长线上一点,∠ABC的平分线与∠ACE的平分线交于点D,若∠A=46°,则∠D的度数为( )
如图,△ABC中,E为边BC延长线上一点,∠ABC的平分线与∠ACE的平分线交于点D,若∠A=46°,则∠D的度数为( )| A. | 46° | B. | 92° | C. | 44° | D. | 23° |
20.顺次连接矩形的四边形中点所得的四边形一定是( )
| A. | 平行四边形 | B. | 矩形 | C. | 菱形 | D. | 正方形 |
17.已知四边形ABCD是平行四边形,下列结论中不正确的是( )
| A. | 当AB=BC时,四边形ABCD是菱形 | B. | 当AC=BD时,四边形是正方形 | ||
| C. | 当∠ABC=90°时,四边形是矩形 | D. | 当AC⊥BD时,四边形是菱形 |
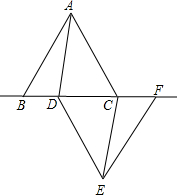 如图,已知△ABC和△DEF是两个边长都为10cm的等边三角形,且B、D、C、F都在同一条直线上,连接AD、CE.
如图,已知△ABC和△DEF是两个边长都为10cm的等边三角形,且B、D、C、F都在同一条直线上,连接AD、CE.