题目内容
5.若正实数x、y、z、r满足:(1)x2+y2=z2;(2)z$\sqrt{{x}^{2}-{r}^{2}}$=x2,求证:xy=zr(提示:可根据条件构造直角三角形和其斜边上的高来证明).分析 由条件(1)可构造直角三角形ABC,使AC=y,BC=x,AB=z,如图,由条件(2)联想射影定理,作斜边AB上的高CD,知CD=r,由三角形面积公式知AB•CD=AC•BC,即xy=zr.
解答  解:设AC=y,BC=x,AB=z
解:设AC=y,BC=x,AB=z
∵x2+y2=z2,
∴△ACB是直角三角形,
设CD是AB边上的高线,
∵z$\sqrt{{x}^{2}-{r}^{2}}$=x2,
∴BD×AB=BC2,
故CD⊥AB,
∴AB•CD=AC•BC,
即xy=zr.
点评 本题考查了勾股定理的逆定理的应用,解此题的关键是根据条件构造直角三角形和其斜边上的高来证明.

练习册系列答案
相关题目
16.不论x取何值时,下列分式总有意义的是( )
| A. | $\frac{2+x}{x}$ | B. | $\frac{{x}^{2}+1}{2x}$ | C. | $\frac{1}{{x}^{2}}$ | D. | $\frac{2x-1}{{x}^{2}+1}$ |
14.已知边长为a的正方形的面积为8,则下列说法中,错误的是( )
| A. | a是无理数 | B. | a是方程x2-8=0的解 | ||
| C. | a是8的算术平方根 | D. | a满足不等式$\frac{2x-4}{3}>1$ |
 如图,点P是直线l:y=-2x-2上的点,过点P的另一条直线m交抛物线y=x2于A、B两点,若点P的坐标为(-2,t),当PA=AB时,求点A的坐标.
如图,点P是直线l:y=-2x-2上的点,过点P的另一条直线m交抛物线y=x2于A、B两点,若点P的坐标为(-2,t),当PA=AB时,求点A的坐标.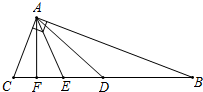 如图,在△ABC中,∠BAC=90°,∠B<22.5°,AD、AE、AF分别是中线、角平分线、高,如果把图中相等的锐角都记为一组,则共有( )
如图,在△ABC中,∠BAC=90°,∠B<22.5°,AD、AE、AF分别是中线、角平分线、高,如果把图中相等的锐角都记为一组,则共有( )
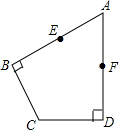 如图,在四边形ABCD中,AB⊥BC,AD⊥CD,AB=AD=6,∠BAD=60°.
如图,在四边形ABCD中,AB⊥BC,AD⊥CD,AB=AD=6,∠BAD=60°.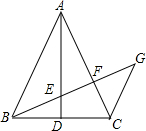 如图所示,在△ABC中,AB=AC,AD⊥BC,CG∥AB,BG分别交AD,AC于E,F.若$\frac{EF}{BE}=\frac{2}{3}$,那么$\frac{GE}{BE}$的值为$\frac{3}{2}$.
如图所示,在△ABC中,AB=AC,AD⊥BC,CG∥AB,BG分别交AD,AC于E,F.若$\frac{EF}{BE}=\frac{2}{3}$,那么$\frac{GE}{BE}$的值为$\frac{3}{2}$.