题目内容
16.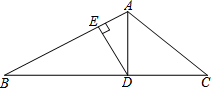 如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,AB=8,DE=4,AC=6,则△ACD的面积为( )
如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,AB=8,DE=4,AC=6,则△ACD的面积为( )| A. | 8 | B. | 10 | C. | 12 | D. | 24 |
分析 作DF⊥AC于F,根据角平分线的性质得到DF=DE=4,根据三角形的面积公式计算即可.
解答 解: 作DF⊥AC于F,
作DF⊥AC于F,
∵AD是∠BAC的角平分线,DE⊥AB,DF⊥AC,
∴DF=DE=4,
∴△ACD的面积=$\frac{1}{2}$×AC×DF=12,
故选:C.
点评 本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
4.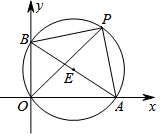 如图,已知A,B两点的坐标分别为(2$\sqrt{3}$,0),(0,2),P是△AOB外接圆上一点,且∠AOP=45°,则P点到x轴的距离为( )
如图,已知A,B两点的坐标分别为(2$\sqrt{3}$,0),(0,2),P是△AOB外接圆上一点,且∠AOP=45°,则P点到x轴的距离为( )
 如图,已知A,B两点的坐标分别为(2$\sqrt{3}$,0),(0,2),P是△AOB外接圆上一点,且∠AOP=45°,则P点到x轴的距离为( )
如图,已知A,B两点的坐标分别为(2$\sqrt{3}$,0),(0,2),P是△AOB外接圆上一点,且∠AOP=45°,则P点到x轴的距离为( )| A. | $\sqrt{6}$ | B. | $2\sqrt{2}$ | C. | $\sqrt{6}+\sqrt{2}$ | D. | $1+\sqrt{3}$ |
11.在平面直角坐标系中,将直线l1:y=-3x-1平移后,得到直线l2:y=-3x+2,则下列平移方式正确的是( )
| A. | 将l1向左平移1个单位 | B. | 将l1向右平移1个单位 | ||
| C. | 将l1向上平移2个单位 | D. | 将l1向上平移1个单位 |
8.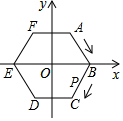 如图,在平面直角坐标系中,六边形ABCDEF是半径为1的正六边形,点O为正六边形ABCDEF的中心,点P从点B出发,沿正六边形按顺时针方向运动,速度为每秒1个单位长度,则第2017秒时,点P的坐标是( )
如图,在平面直角坐标系中,六边形ABCDEF是半径为1的正六边形,点O为正六边形ABCDEF的中心,点P从点B出发,沿正六边形按顺时针方向运动,速度为每秒1个单位长度,则第2017秒时,点P的坐标是( )
 如图,在平面直角坐标系中,六边形ABCDEF是半径为1的正六边形,点O为正六边形ABCDEF的中心,点P从点B出发,沿正六边形按顺时针方向运动,速度为每秒1个单位长度,则第2017秒时,点P的坐标是( )
如图,在平面直角坐标系中,六边形ABCDEF是半径为1的正六边形,点O为正六边形ABCDEF的中心,点P从点B出发,沿正六边形按顺时针方向运动,速度为每秒1个单位长度,则第2017秒时,点P的坐标是( )| A. | ($\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$) | B. | (-1,0) | C. | (-$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$) | D. | ($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$) |
5.有理数$\frac{1}{3}$的相反数是( )
| A. | $\frac{1}{3}$ | B. | 3 | C. | -3 | D. | -$\frac{1}{3}$ |
6.不等式组$\left\{\begin{array}{l}\frac{1}{2}x-1<\frac{x}{3}\;,\;\;\\ 2x-4<3x+3.\end{array}\right.$的解集为( )
| A. | -7<x<6 | B. | -7<x<1 | C. | x<1 | D. | x<6 |
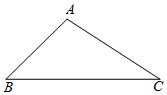 如图,在△ABC中,∠B=45°,∠C=30°,AB=4$\sqrt{2}$,求AC和BC的长.
如图,在△ABC中,∠B=45°,∠C=30°,AB=4$\sqrt{2}$,求AC和BC的长.