题目内容
10.在三角形纸片ABC中,已知∠ABC=90°,AB=5,BC=12.过点A作直线l平行于BC,折叠三角形纸片ABC,使直角顶点B落在直线l上的T处,折痕为MN.当点T在直线l上移动时,折痕的端点M、N也随之移动.若限定端点M、N分别在AB、BC边上移动,则线段AT长度的最大值与最小值之和为17-$\sqrt{119}$(计算结果不取近似值).分析 找到两个极端,即AT取最大或最小值时,点M或N的位置,分别求出点M与A重合时,AT取最大值,当点N与C重合时,AT有最小值.
解答 解:如图所示:当点M与点A重合时,AT取得最大值,
由轴对称可知,AT=AB=5;
当点N与点C重合时,AT取得最小值,
过点C作CD⊥l于点D,连结CT,则四边形ABCD为矩形,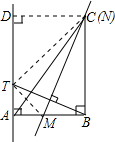 ∴CD=AB=5,
∴CD=AB=5,
由轴对称可知,CT=BC=12,
在Rt△CDT中,CD=5,CT=12,
则DT=$\sqrt{1{2}^{2}-{5}^{2}}$=$\sqrt{119}$,
∴AT=AD-DT=12-$\sqrt{119}$,
综上可得:线段AT长度的最大值与最小值的和为17-$\sqrt{119}$;
故答案为:17-$\sqrt{119}$.
点评 本题考查了学生的动手能力及图形的折叠、勾股定理的应用等知识,难度稍大,学生主要缺乏动手操作习惯,单凭想象容易造成错误.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.下列各组角中,∠1与∠2是对顶角的为( )
| A. |  | B. |  | C. |  | D. |  |
1.某市为美化城市,有关部门决定利用现有的4200盆甲种花卉和3090盆乙种花卉,搭配成A、B两种园艺造型共60个,摆放于主干街道的两侧,搭配每个造型所需花卉数量的情况如下表所示,结合上述信息,解答下列问题:
(1)符合题意的搭配方案有几种?
(2)如果搭配一个A种造型的成本为600元,搭配一个B种造型的成本为800元,试说明选用那种方案成本最低?最低成本为多少元?
| 造型花卉 | 甲 | 乙 |
| A | 80 | 40 |
| B | 50 | 70 |
(2)如果搭配一个A种造型的成本为600元,搭配一个B种造型的成本为800元,试说明选用那种方案成本最低?最低成本为多少元?
 如图,在△ABC中,∠A=50°,∠B=70°,点D在BC的延长线上,那么∠ACD=120°.
如图,在△ABC中,∠A=50°,∠B=70°,点D在BC的延长线上,那么∠ACD=120°. 如图,梯形ABCD中,AD∥BC,AC为对角线,且∠DCA=∠B,线段AD、BC的长是方程x(x-4)+2(4-x)=0的两根,且AD<BC,CD=3,求AB与AC的长.
如图,梯形ABCD中,AD∥BC,AC为对角线,且∠DCA=∠B,线段AD、BC的长是方程x(x-4)+2(4-x)=0的两根,且AD<BC,CD=3,求AB与AC的长. 如图,在△ABC中,AC=8,D、E分别为AB、AC的中点,F为线段DE上一点,连接AF、CF使AF⊥CF,且DF=1.若△ADF面积为2,则△ABC的面积为( )
如图,在△ABC中,AC=8,D、E分别为AB、AC的中点,F为线段DE上一点,连接AF、CF使AF⊥CF,且DF=1.若△ADF面积为2,则△ABC的面积为( )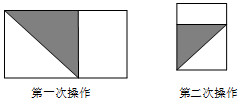 将长为1,宽为a的长方形纸片$({\frac{1}{2}<a<1})$如图那样折一下,剪下一个边长等于长方形的宽度的正方形(称为第一次操作);再把剩下的长方形如图那样折一下,剪下一个边长等于此时长方形宽度的正方形(称为第二次操作);如些反复操作下去,若在第n次操作后剩下的长方形为正方形,则操作终止.
将长为1,宽为a的长方形纸片$({\frac{1}{2}<a<1})$如图那样折一下,剪下一个边长等于长方形的宽度的正方形(称为第一次操作);再把剩下的长方形如图那样折一下,剪下一个边长等于此时长方形宽度的正方形(称为第二次操作);如些反复操作下去,若在第n次操作后剩下的长方形为正方形,则操作终止.