题目内容
2．
如图，在△ABC中，AC=8，D、E分别为AB、AC的中点，F为线段DE上一点，连接AF、CF使AF⊥CF，且DF=1．若△ADF面积为2，则△ABC的面积为（ ）| A． | 25 | B． | 30 | C． | 35 | D． | 40 |
分析 根据直角三角形的性质求出EF的长，利用三角形中位线定理可求出DE∥BC，DE=$\frac{1}{2}$BC，证出△ADE∽△ABC，得出面积比为1：4，求出△ADE的面积，进而可求△ABC的面积．
解答 解：∵D、E分别为AB、AC的中点，
∴DE∥BC，DE=$\frac{1}{2}$BC，
∴△ADE∽△ABC，相似比为$\frac{1}{2}$，
∴△ADE的面积：△ABC的面积=1：4，
∵AF⊥CF，
∴EF=$\frac{1}{2}$AC=4，
∵DF=1，
∴△AEF的面积=4△ADF的面积=8，
∴△ADE的面积=2+8=10，
∴△ABC的面积=4×10=40；
故选：D．
点评 本题考查了三角形的中位线定理和直角三角形斜边上的中线性质以及相似三角形的判定与性质；熟练掌握三角形中位线定理，证明三角形相似是解决问题的关键．
练习册系列答案
相关题目
在平面直角坐标系xOy中，抛物线y=mx2-2mx+m-2（m≠0）的顶点为A，与x轴交于B，C两点（点B在点C左侧），与y轴负半轴交于点D．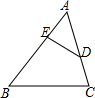
如图，∠ADE=∠B，若AD：AB=2：3，则△ADE与△ABC的面积比为4：9．
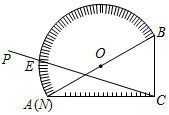如图，量角器的直径与直角三角板ABC的斜边AB重合，其中量角器0刻度线的端点N与点A重合，射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转，CP与量角器的半圆弧交于点E，第23秒时，点E在量角器上对应的度数是92度．