题目内容
1.某市为美化城市,有关部门决定利用现有的4200盆甲种花卉和3090盆乙种花卉,搭配成A、B两种园艺造型共60个,摆放于主干街道的两侧,搭配每个造型所需花卉数量的情况如下表所示,结合上述信息,解答下列问题:| 造型花卉 | 甲 | 乙 |
| A | 80 | 40 |
| B | 50 | 70 |
(2)如果搭配一个A种造型的成本为600元,搭配一个B种造型的成本为800元,试说明选用那种方案成本最低?最低成本为多少元?
分析 (1)设需要搭配x个A种造型,则需要搭配B种造型(60-x)个,根据“4200盆甲种花卉”“3090盆乙种花卉”列不等式求解,取整数值即可.
(2)计算出每种方案的花费,然后即可判断出答案.
解答 解:(1)设需要搭配x个A种造型,则需要搭配B种造型(60-x)个,
则有 $\left\{\begin{array}{l}{80x+50(60-x)≤4200}\\{40x+70(60-x)≤3090}\end{array}\right.$,
解得37≤x≤40,
所以x=37或38或39或40.
第一种方案:A种造型37个,B种造型23个;
第二种方案:A种造型38个,B种造型22个;
第三种方案:A种造型39个,B种造型21个.
第四种方案:A种造型40个,B种造型20个;
(2)分别计算四种方案的成本为:
①37×600+23×800=40600元,
②38×600+22×800=40400元,
③39×600+21×800=40200元,
④40×600+20×800=40000元.
通过比较可知第④种方案成本最低.
答:选择第四种方案成本最低,最低为40000元.
点评 此题考查了一元一次不等式组的应用,是一道实际问题,有一定的开放性,(1)根据图表信息,利用所用花卉数量不超过甲、乙两种花卉的最高数量列不等式组解答;(2)为最优化问题,根据(1)的结果直接计算即可.

练习册系列答案
相关题目
 在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-2(m≠0)的顶点为A,与x轴交于B,C两点(点B在点C左侧),与y轴负半轴交于点D.
在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-2(m≠0)的顶点为A,与x轴交于B,C两点(点B在点C左侧),与y轴负半轴交于点D. 如图,PQ是⊙O的切线,Q是切点,若OQ=5,OP=9,则∠P的度数是34°(结果精确到1°).
如图,PQ是⊙O的切线,Q是切点,若OQ=5,OP=9,则∠P的度数是34°(结果精确到1°).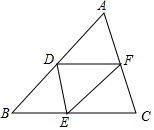 如图,在△ABC中,D,E,F分别是AB,BC,CA的中点,以这些点为顶点,在图中,你能画出多少个平行四边形?为什么?
如图,在△ABC中,D,E,F分别是AB,BC,CA的中点,以这些点为顶点,在图中,你能画出多少个平行四边形?为什么? 如图,AD是Rt△ABC斜边上的高,若AB=2,BC=6,求BD的长.
如图,AD是Rt△ABC斜边上的高,若AB=2,BC=6,求BD的长.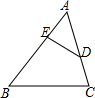 如图,∠ADE=∠B,若AD:AB=2:3,则△ADE与△ABC的面积比为4:9.
如图,∠ADE=∠B,若AD:AB=2:3,则△ADE与△ABC的面积比为4:9.