题目内容
15.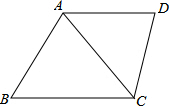 如图,梯形ABCD中,AD∥BC,AC为对角线,且∠DCA=∠B,线段AD、BC的长是方程x(x-4)+2(4-x)=0的两根,且AD<BC,CD=3,求AB与AC的长.
如图,梯形ABCD中,AD∥BC,AC为对角线,且∠DCA=∠B,线段AD、BC的长是方程x(x-4)+2(4-x)=0的两根,且AD<BC,CD=3,求AB与AC的长.
分析 首先解方程求得AD和BC的长,然后得到△ABC∽△DCA,根据相似三角形对应边的比相等列式计算即可.
解答 解:∵线段AD、BC的长是方程x(x-4)+2(4-x)=0的两根,且AD<BC,
∴AD=2,BC=4,
∵AD∥BC,
∴∠DAC=∠BCA,
∵∠DCA=∠B,
∴△ABC∽△DCA,
∴$\frac{AB}{DC}=\frac{AC}{AD}=\frac{BC}{AC}$,
即:$\frac{AB}{3}=\frac{AC}{2}=\frac{4}{AC}$,
解得:AB=3$\sqrt{2}$,AC=2$\sqrt{2}$.
点评 本题考查了相似三角形的判定与性质、解一元二次方程及梯形的知识,解题的关键是能够得到相似三角形,并正确的确定对应边,难度不大.

练习册系列答案
相关题目
3.若关于x的方程(m-2)x2+mx-1=0是一元二次方程,则m的取值范围是( )
| A. | m≠2 | B. | m=2 | C. | m≥2 | D. | m≠0 |
 如图,AD是Rt△ABC斜边上的高,若AB=2,BC=6,求BD的长.
如图,AD是Rt△ABC斜边上的高,若AB=2,BC=6,求BD的长.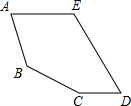 聪聪用五根宽度相同的木条拼成了一个五边形,如图所示,已知AE∥CD,∠A=$\frac{1}{2}$∠C,∠B=120°,∠D=50°.
聪聪用五根宽度相同的木条拼成了一个五边形,如图所示,已知AE∥CD,∠A=$\frac{1}{2}$∠C,∠B=120°,∠D=50°. 如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1,还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2015次操作后得到的折痕D2014E2014,到BC的距离记为h2015;若h1=1,则h2016的值为2-$\frac{1}{{2}^{2015}}$.
如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1,还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2015次操作后得到的折痕D2014E2014,到BC的距离记为h2015;若h1=1,则h2016的值为2-$\frac{1}{{2}^{2015}}$.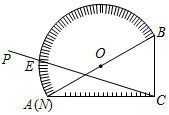 如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,第23秒时,点E在量角器上对应的度数是92度.
如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,第23秒时,点E在量角器上对应的度数是92度.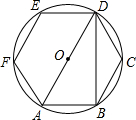 如图,正六边形ABCDEF内接于⊙O,连接AD、BD,则∠DAB的余弦值是$\frac{1}{2}$.
如图,正六边形ABCDEF内接于⊙O,连接AD、BD,则∠DAB的余弦值是$\frac{1}{2}$.