题目内容
16．
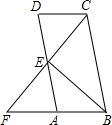如图，在?ABCD中，BC=2CD，E为AD的中点，CE，BA的延长线交于点F，求证：∠F=∠BCF．
分析 根据中点定义和平行四边形的对边相等得：AD=BC=2CD=2DE，则DE=CD，得∠DCE=∠DEC，再由平行线的性质：内错角相等可得结论．
解答 证明：∵E为AD的中点，
∴AD=2DE，
∵四边形ABCD是平行四边形，
∴AD=BC，
∴BC=2DE，
∵BC=2CD，
∴DE=CD，
∴∠DCE=∠DEC，
∵AB∥CD，AD∥BC，
∴∠DCF=∠F，∠DEC=∠BCF，
∴∠F=∠BCF．
点评 本题考查了平行四边形的性质和平行线的性质、等腰三角形的性质，属于基础题，熟练掌握平行四边形的性质是关键．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
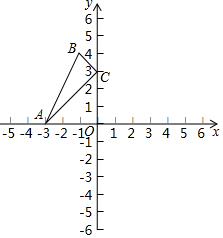已知点A（-3，0），点C（0，3）且点B的坐标为（-1，4），计算△ABC的面积．
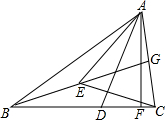如图，在△ABC中，∠BAC=60°，∠ACB=80°，AD为∠BAC的角平分线，G、E分别是AC、BG的中点，AF⊥BC于F．求：
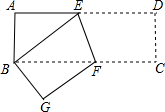如图，在矩形纸片ABCD中，AD=9，AB=3，将其折叠，使点D与点B重合，折痕为EF，求折叠后DE的长和折痕EF的长．