题目内容
2．
如图，如图，点A（3，m）在第一象限，OA与x轴所夹的锐角为∠1，tan∠1=$\frac{2}{3}$，则m的值是2．
分析 作AB⊥x轴于点B，根据正切函数的定义即可求解．
解答 
解：作AB⊥x轴于点B．
∵A的坐标是（3，m），
∴OB=3，AB=m．
又∵tan∠1=$\frac{AB}{OB}$=$\frac{2}{3}$，即$\frac{m}{3}$=$\frac{2}{3}$，
∴m=2．
故答案是：2．
点评 本题考查了正切的定义以及平面直角坐标系，理解正切的定义是关键．
练习册系列答案
相关题目
如图，A、B、C是⊙O上的三点，若∠C=30°，OA=3，则弧AB的长为π．（结果保留π）
17．
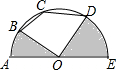如图，半圆O的直径AE=8，点B，C，D均在半圆上，若AB=BC，CD=DE，连接OB，OD，则图中阴影部分的面积为（ ）
如图，半圆O的直径AE=8，点B，C，D均在半圆上，若AB=BC，CD=DE，连接OB，OD，则图中阴影部分的面积为（ ）| A． | 2π | B． | 4π | C． | 8π | D． | 16π |
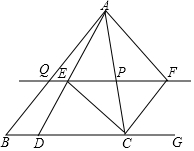如图，在△ABC 中，点P是AC边上的一点，过点P作与BC平行的直线PQ，交AB于点Q，点D在线段 BC上，联接AD交线段PQ于点E，且$\frac{CP}{CD}$=$\frac{QE}{BD}$，点G在BC延长线上，∠ACG的平分线交直线PQ于点F．