题目内容
12.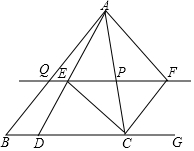 如图,在△ABC 中,点P是AC边上的一点,过点P作与BC平行的直线PQ,交AB于点Q,点D在线段 BC上,联接AD交线段PQ于点E,且$\frac{CP}{CD}$=$\frac{QE}{BD}$,点G在BC延长线上,∠ACG的平分线交直线PQ于点F.
如图,在△ABC 中,点P是AC边上的一点,过点P作与BC平行的直线PQ,交AB于点Q,点D在线段 BC上,联接AD交线段PQ于点E,且$\frac{CP}{CD}$=$\frac{QE}{BD}$,点G在BC延长线上,∠ACG的平分线交直线PQ于点F.(1)求证:PC=PE;
(2)当P是边AC的中点时,求证:四边形AECF是矩形.
分析 (1)根据相似三角形的性质得到$\frac{QE}{BD}$=$\frac{AE}{AD}$,$\frac{PE}{CD}=\frac{AE}{AD}$,等量代换得到$\frac{PE}{CD}$=$\frac{QE}{BD}$,推出$\frac{CP}{CD}$=$\frac{PE}{CD}$,于是得到结论;
(2)根据平行线的性质得到∠PFC=∠FCG,根据角平分线的性质得到∠PCF=∠FCG,等量代换得到∠PFC=∠FCG,根据等腰三角形的性质得到PF=PC,得到PF=PE,由已知条件得到AP=CP,推出四边形AECF是平行四边形,于是得到结论.
解答 (1)证明:∵PQ∥BC,
∴△AQE∽△ABD,△AEP∽△ADC,
∴$\frac{QE}{BD}$=$\frac{AE}{AD}$,$\frac{PE}{CD}=\frac{AE}{AD}$,
∴$\frac{PE}{CD}$=$\frac{QE}{BD}$,
∵$\frac{CP}{CD}$=$\frac{QE}{BD}$,
∴$\frac{CP}{CD}$=$\frac{PE}{CD}$,
∴PC=PE;
(2)∵PF∥DG,
∴∠PFC=∠FCG,
∵CF平分∠PCG,
∴∠PCF=∠FCG,
∴∠PFC=∠FCG,
∴PF=PC,
∴PF=PE,
∵P是边AC的中点,
∴AP=CP,
∴四边形AECF是平行四边形,
∵PQ∥CD,
∴∠PEC=∠DCE,
∴∠PCE=∠DCE,
∴∠PCE+∠PCF=$\frac{1}{2}$(∠PCD+∠PCG)=90°,
∴∠ECF=90°,
∴平行四边形AECF是矩形.
点评 本题考查了相似三角形的判定和性质,平行四边形的判定和性质,矩形的判定,等腰三角形的性质,熟练掌握相似三角形的性质是解题的关键.

 如图,如图,点A(3,m)在第一象限,OA与x轴所夹的锐角为∠1,tan∠1=$\frac{2}{3}$,则m的值是2.
如图,如图,点A(3,m)在第一象限,OA与x轴所夹的锐角为∠1,tan∠1=$\frac{2}{3}$,则m的值是2. 如图,△ABC中,∠ACB=90°,D在AB上,若AD=AC,且∠A=50°,则∠DCB的度数为25°.
如图,△ABC中,∠ACB=90°,D在AB上,若AD=AC,且∠A=50°,则∠DCB的度数为25°.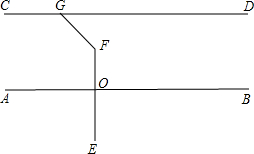 如图:已知AB∥CD,EF⊥AB于点O,∠FGC=131°,求∠EFG的度数.
如图:已知AB∥CD,EF⊥AB于点O,∠FGC=131°,求∠EFG的度数.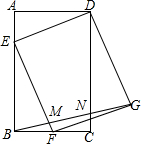 如图,在矩形ABCD中,AB=3,BC=2,点F是BC的中点,点E是边AB上一点,且BE=2,连结DE,EF,并以DE,EF为边作?EFGD,连结BG,分别交EF和DC于点M,N,则$\frac{BM}{NG}$=$\frac{6}{7}$.
如图,在矩形ABCD中,AB=3,BC=2,点F是BC的中点,点E是边AB上一点,且BE=2,连结DE,EF,并以DE,EF为边作?EFGD,连结BG,分别交EF和DC于点M,N,则$\frac{BM}{NG}$=$\frac{6}{7}$.
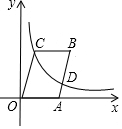 已知:如图,在平面直角坐标系xOy中,点A在x轴的正半轴上,点B、C在第一象限,且四边形OABC是平行四边形,OC=2$\sqrt{5}$,sin∠AOC=$\frac{2}{5}$$\sqrt{5}$,反比例函数y=$\frac{k}{x}$的图象经过点C以及边AB的中点D.
已知:如图,在平面直角坐标系xOy中,点A在x轴的正半轴上,点B、C在第一象限,且四边形OABC是平行四边形,OC=2$\sqrt{5}$,sin∠AOC=$\frac{2}{5}$$\sqrt{5}$,反比例函数y=$\frac{k}{x}$的图象经过点C以及边AB的中点D.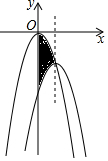 如图,在平面直角坐标系中,二次函数y=-3x2的图象经过平移得到二次函数y=-3x2+6x-6的图象,则二次函数y=-3x2图象的对称轴与两段抛物线所围成的阴影部分的面积为3.
如图,在平面直角坐标系中,二次函数y=-3x2的图象经过平移得到二次函数y=-3x2+6x-6的图象,则二次函数y=-3x2图象的对称轴与两段抛物线所围成的阴影部分的面积为3.