题目内容
6. 如图,在平面直角坐标系中,四边形OABC为矩形,其中A(2,0)C(0,4),反比例函数y=$\frac{k}{x}$(x>0,k>0)的图象与矩形的对角线AC有公共点,并且交AB边于点E,交BC边于点F,以下结论:①直线AC的解析式为y=-2x+4;②EF∥AC;③当反比例函数图象与线段AC只有一个公共点时,k值最大,最大值为2;④△BEF面积的最小值为2.则下列选项中,正确的是( )
如图,在平面直角坐标系中,四边形OABC为矩形,其中A(2,0)C(0,4),反比例函数y=$\frac{k}{x}$(x>0,k>0)的图象与矩形的对角线AC有公共点,并且交AB边于点E,交BC边于点F,以下结论:①直线AC的解析式为y=-2x+4;②EF∥AC;③当反比例函数图象与线段AC只有一个公共点时,k值最大,最大值为2;④△BEF面积的最小值为2.则下列选项中,正确的是( )| A. | ②③④ | B. | ①③④ | C. | ①②④ | D. | ①②③ |
分析 ①由点A、B的坐标利用待定系数法即可求出直线AC的解析式,①成立;②由反比例函数图象上点的坐标特征求出点E、F的坐标,根据$\frac{BE}{BA}$=$\frac{BF}{BC}$=$\frac{8-k}{8}$,即可得出EF∥AC,②成立;③设反比例函数图象与AC的交点为D,过D作DM⊥x轴于点M,过点D作DN⊥y轴于点N,设OM=x(0<x<2),则ON=4-2x,根据反比例函数图象上点的坐标特征即可得出k=-2(x-1)2+2≥2,由此可得出k的最小值,再将直线AC解析式代入反比例函数解析式整理出一元二次方程,通过解方程组即可得出此时反比例函数图象与线段AC只有一个公共点,③成立;④根据三角形的面积公式结合k的取值范围即可得出S△BEF≥$\frac{9}{4}$,④不成立.综上即可得出结论.
解答 解:①设直线AC的解析式为y=ax+b,
将A(2,0)、B(0,4)代入y=ax+b,
$\left\{\begin{array}{l}{2a+b=0}\\{b=4}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=-2}\\{b=4}\end{array}\right.$,
∴直线AC的解析式为y=-2x+4,①成立;
②当x=2时,y=$\frac{k}{x}$=$\frac{k}{2}$,
∴点E(2,$\frac{k}{2}$);
当y=$\frac{k}{x}$=4时,x=$\frac{k}{4}$,
∴点F($\frac{k}{4}$,4).
∵四边形OABC为矩形,其中A(2,0)C(0,4),
∴点B(2,4),
∴BC=2,BA=4,BF=2-$\frac{k}{4}$=$\frac{8-k}{4}$,BE=4-$\frac{k}{2}$=$\frac{8-k}{2}$,
∴$\frac{BE}{BA}$=$\frac{BF}{BC}$=$\frac{8-k}{8}$,
∴EF∥AC,②成立;
③设反比例函数图象与AC的交点为D,过D作DM⊥x轴于点M,过点D作DN⊥y轴于点N,如图所示.
设OM=x(0<x<2),则ON=4-2x,
∴k=x(4-2x)=-2(x-1)2+2,
当x=1时,k取最大值,最大值为2.
将y=-2x+4代入y=$\frac{2}{x}$中,整理得:x2-2x+1=(x-1)2=0,
∴当反比例函数图象与线段AC只有一个公共点时,k值最大,最大值为2,③成立;
④∵S△BEF=$\frac{1}{2}$BE•BF=$\frac{(8-k)^{2}}{16}$≥$\frac{9}{4}$,
∴△BEF面积的最小值为$\frac{9}{4}$,④不成立.
故选D.
点评 本题考查了矩形的性质、反比例函数图象上点的坐标特征以及三角形的面积,逐一分析四条结论的正确与否是解题的关键.

| A. | 1 | B. | 0 | C. | 0.5 | D. | -1 |
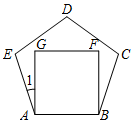 有一个正五边形和一个正方形边长相等,如图放置,则∠1=18°.
有一个正五边形和一个正方形边长相等,如图放置,则∠1=18°.