题目内容
13.我们知道:分式和分数有着很多的相似点,如类比分数的基本性质,我们得到了分式的基本性质:类比分数的运算法则,我们得到了分式的运算法则,等等.小学里,把分子比分母小的分数叫做真分数.类似地,我们把分子整式的次数小于分母整式的次数的分式称为真分式;反之,称为假分式,对于任何一个假分式都可以化成整式与真分式的和的形式.如:$\frac{x+1}{x-1}$=$\frac{x-1+2}{x-1}$=$\frac{x-1}{x-1}$+$\frac{2}{x-1}$=1+$\frac{2}{x-1}$;
$\frac{2x-3}{x+1}$=$\frac{2x+2-5}{x+1}$=$\frac{2x+2}{x+1}$+$\frac{-5}{x+1}$=2+(-$\frac{5}{x+1}$).
(1)下列分式中:①$\frac{x-1}{x+1}$,②$\frac{{x}^{2}}{x-1}$,③$\frac{4y}{2{y}^{2}+1}$,④$\frac{{m}^{2}+3}{{m}^{2}-1}$,属于真分式的是③(填序号);
(2)将假分式$\frac{4a+5}{2a-1}$化成整式与真分式的和的形式为:
$\frac{4a+5}{2a-1}$=2+$\frac{7}{2a-1}$,若假分式$\frac{4a+5}{2a-1}$的值为整数,则整数a的值为1或0或4或-3;
(3)将假分式$\frac{{a}^{2}-3}{a+1}$化成整式与真分式的和的形式.
分析 (1)根据真分式的定义即可作出判断;
(2)利用例题的方法即可将假分式$\frac{4a+5}{2a-1}$化成整式与真分式的和,假分式$\frac{4a+5}{2a-1}$的值为整数,则化成整式与真分式的和后,所得真分式的分母是分式的分子的因数,据此列方程求解;
(3)把分式的分子利用含分母的式子表示出来,先化成整式与分子和分母同此的形式,然后化成真分式的形式.
解答 解:(1)根据真分式的定义,满足条件的只有③,故答案是③;
(2)$\frac{4a+5}{2a-1}$=$\frac{4a-2+7}{2a-1}$=$\frac{4a-2}{2a-1}$+$\frac{7}{2a-1}$.
若分式$\frac{4a+5}{2a-1}$的值为整数,则2a-1=±1或±7,则a=1或0或4或-3.
故答案是:2; $\frac{2}{2a-1}$; 1或0或4或-3;
(3)$\frac{{a}^{2}-3}{a+1}$=$\frac{{a}^{2}+a-a-3}{a+1}$=$\frac{a(a+1)}{a+1}$+$\frac{a-3}{a+1}$=a+$\frac{a+1-4}{a+1}$=a+$\frac{a+1}{a+1}$-$\frac{4}{a+1}$=a+1-$\frac{4}{a+1}$.
点评 本题考查了分式的化简,正确理解题意,理解把假分式化成真分式的思路是关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
15.用配方法解一元二次方程x2+6x-3=0,原方程可变形为( )
| A. | (x+3)2=3 | B. | (x+3)2=6 | C. | (x+3)2=12 | D. | (x+3)2=9 |
4.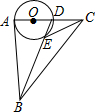 如图,△ABC中,∠BAC=90°,AB=AC=2,D为AC上一动点,以AD为直径的⊙O交BD于E,则线段CE的最小值为( )
如图,△ABC中,∠BAC=90°,AB=AC=2,D为AC上一动点,以AD为直径的⊙O交BD于E,则线段CE的最小值为( )
 如图,△ABC中,∠BAC=90°,AB=AC=2,D为AC上一动点,以AD为直径的⊙O交BD于E,则线段CE的最小值为( )
如图,△ABC中,∠BAC=90°,AB=AC=2,D为AC上一动点,以AD为直径的⊙O交BD于E,则线段CE的最小值为( )| A. | $\sqrt{5}$ | B. | $\sqrt{5}$+1 | C. | 2$\sqrt{5}$ | D. | $\sqrt{5}$-1 |
1.下列条件中,不能判断两个三角形全等的方法有( )
| A. | 两边和一个角分别相等的两个三角形 | |
| B. | 两个角及其夹边分别相等的两个三角形 | |
| C. | 三边分别相等的两个三角形 | |
| D. | 斜边和一条直角边分别相等的两个直角三角形 |
 如图△ABC中,∠D=90°,C是BD上一点,已知CB=9,AB=17,AC=10,则DC的长是6,AD=8.
如图△ABC中,∠D=90°,C是BD上一点,已知CB=9,AB=17,AC=10,则DC的长是6,AD=8.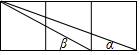 如图,在边长为1的正方形网格内连结不同的对角线得到∠α和∠β,则∠α+∠β=45度.
如图,在边长为1的正方形网格内连结不同的对角线得到∠α和∠β,则∠α+∠β=45度.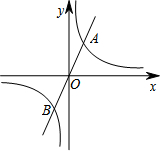 如图,直线y=kx(k>0)与双曲线y=$\frac{3}{x}$交于A、B两点,若A、B两点的坐标分别为A(x1,y1),B(x2,y2),则x1y2+x2y1的值为-6.
如图,直线y=kx(k>0)与双曲线y=$\frac{3}{x}$交于A、B两点,若A、B两点的坐标分别为A(x1,y1),B(x2,y2),则x1y2+x2y1的值为-6.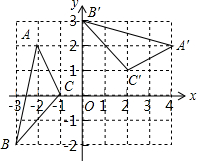 如图,在平面直角坐标系xOy中,每个小方格的边长为1,将△ABC绕点P旋转得到△A′B′C′,则点P的坐标为(1,-1).
如图,在平面直角坐标系xOy中,每个小方格的边长为1,将△ABC绕点P旋转得到△A′B′C′,则点P的坐标为(1,-1).