题目内容
20.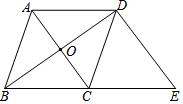 如图,在菱形ABCD中,对角线AC、BD相交于点O,且AB=5,AC=6,过点D作AC的平行线交BC的延长线于点E,则△BDE的面积为24.
如图,在菱形ABCD中,对角线AC、BD相交于点O,且AB=5,AC=6,过点D作AC的平行线交BC的延长线于点E,则△BDE的面积为24.
分析 先判断出四边形ACED是平行四边形,从而得出DE的长度,根据菱形的性质求出BD的长度,利用勾股定理的逆定理可得出△BDE是直角三角形,计算出面积即可.
解答 解:∵AD∥BE,AC∥DE,
∴四边形ACED是平行四边形,
∴AC=DE=6,
在RT△BCO中,BO=$\sqrt{A{B}^{2}-A{O}^{2}}$=4,即可得BD=8,
又∵BE=BC+CE=BC+AD=10,
∴△BDE是直角三角形,
∴S△BDE=$\frac{1}{2}$DE•BD=24.
故答案为:24.
点评 此题考查了菱形的性质、勾股定理的逆定理及三角形的面积,属于基础题,求出BD的长度,判断△BDE是直角三角形,是解答本题的关键.

练习册系列答案
相关题目
2. 如图,在菱形ABCD中,AB=5,∠B=60°,则对角线AC的长等于( )
如图,在菱形ABCD中,AB=5,∠B=60°,则对角线AC的长等于( )
 如图,在菱形ABCD中,AB=5,∠B=60°,则对角线AC的长等于( )
如图,在菱形ABCD中,AB=5,∠B=60°,则对角线AC的长等于( )| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
 如图△ABC中,∠D=90°,C是BD上一点,已知CB=9,AB=17,AC=10,则DC的长是6,AD=8.
如图△ABC中,∠D=90°,C是BD上一点,已知CB=9,AB=17,AC=10,则DC的长是6,AD=8.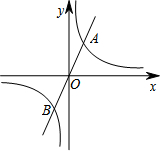 如图,直线y=kx(k>0)与双曲线y=$\frac{3}{x}$交于A、B两点,若A、B两点的坐标分别为A(x1,y1),B(x2,y2),则x1y2+x2y1的值为-6.
如图,直线y=kx(k>0)与双曲线y=$\frac{3}{x}$交于A、B两点,若A、B两点的坐标分别为A(x1,y1),B(x2,y2),则x1y2+x2y1的值为-6. 如图,请用尺规作出圆O的内接正方形(保留作图痕迹,不写作法)
如图,请用尺规作出圆O的内接正方形(保留作图痕迹,不写作法) 如图,AB=DC,请补充一个条件:AC=BD使△ABC≌△DCB.(填其中一种即可)
如图,AB=DC,请补充一个条件:AC=BD使△ABC≌△DCB.(填其中一种即可) 如图,△ABC中,AB=4,∠BAC=30°,若在AC、AB上各取一点M、N使BM+MN的值最小,则这个最小值为2$\sqrt{3}$.
如图,△ABC中,AB=4,∠BAC=30°,若在AC、AB上各取一点M、N使BM+MN的值最小,则这个最小值为2$\sqrt{3}$.