题目内容
10.为了解西安市的交通状况,交通部分对某路段的车流速度v(千米/小时)和车流密度x(辆/千米)进行调查.调查显示;当20≤x≤220时,车流速度v是车流密度x的一次函数,当该路段上的车流密度达到220辆/千米的时候就造成交通堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为80千米/小时.(1)当20≤x≤220时,求v关于x的函数解析式;
(2)求该路段车流密度为150辆/千米时的车流速度.
分析 (1)当20≤x≤220时,设v与x的一次函数关系为v=kx+b (k≠0 ),把(220,0)和(20,80)代入列方程组求出即可;
(2)将x=150代入解析式即可.
解答 解:(1)当0≤x≤20时,v=80;
当20≤x≤220时,设v与x的一次函数关系为v=kx+b (k≠0 ),
由已知得$\left\{\begin{array}{l}{220x+b=0}\\{20x+b=80}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{2}{5}}\\{b=88}\end{array}\right.$,
∴当20≤x≤220时,v关于x的函数解析式为:v=-$\frac{2}{5}$x+88;
(2)依题意,当x=150时,v=-$\frac{2}{5}$×150+88=-60+88=28,
故当车流密度为150辆/千米时,车流速度为28千米/小时.
点评 此题主要考查了一次函数的应用以及待定系数法求一次函数解析式等知识,注意自变量取值范围不同函数解析式不同.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
12.下面各种说法中正确的是( )
| A. | 两数的差一定小于被减数 | |
| B. | 两数的和一定大于每一个加数 | |
| C. | 两数的绝对值相等,这两个数也一定相等 | |
| D. | 两数的积不一定比每一个因数大 |
1.下列条件中,不能判断两个三角形全等的方法有( )
| A. | 两边和一个角分别相等的两个三角形 | |
| B. | 两个角及其夹边分别相等的两个三角形 | |
| C. | 三边分别相等的两个三角形 | |
| D. | 斜边和一条直角边分别相等的两个直角三角形 |
15.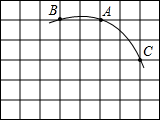 如图,一圆弧过方格的格点A、B、C,试在方格中建立平面直角坐标系,使点A的坐标为(-2,3),则该圆弧所在圆的圆心坐标是( )
如图,一圆弧过方格的格点A、B、C,试在方格中建立平面直角坐标系,使点A的坐标为(-2,3),则该圆弧所在圆的圆心坐标是( )
 如图,一圆弧过方格的格点A、B、C,试在方格中建立平面直角坐标系,使点A的坐标为(-2,3),则该圆弧所在圆的圆心坐标是( )
如图,一圆弧过方格的格点A、B、C,试在方格中建立平面直角坐标系,使点A的坐标为(-2,3),则该圆弧所在圆的圆心坐标是( )| A. | (-1,1) | B. | (0,1) | C. | (-3,1) | D. | (-3,0) |
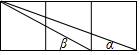 如图,在边长为1的正方形网格内连结不同的对角线得到∠α和∠β,则∠α+∠β=45度.
如图,在边长为1的正方形网格内连结不同的对角线得到∠α和∠β,则∠α+∠β=45度.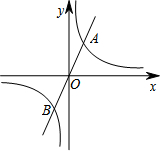 如图,直线y=kx(k>0)与双曲线y=$\frac{3}{x}$交于A、B两点,若A、B两点的坐标分别为A(x1,y1),B(x2,y2),则x1y2+x2y1的值为-6.
如图,直线y=kx(k>0)与双曲线y=$\frac{3}{x}$交于A、B两点,若A、B两点的坐标分别为A(x1,y1),B(x2,y2),则x1y2+x2y1的值为-6.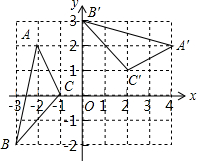 如图,在平面直角坐标系xOy中,每个小方格的边长为1,将△ABC绕点P旋转得到△A′B′C′,则点P的坐标为(1,-1).
如图,在平面直角坐标系xOy中,每个小方格的边长为1,将△ABC绕点P旋转得到△A′B′C′,则点P的坐标为(1,-1). 如图,∵∠1=∠2,∴AB∥DE(同位角相等,两直线平行)
如图,∵∠1=∠2,∴AB∥DE(同位角相等,两直线平行)